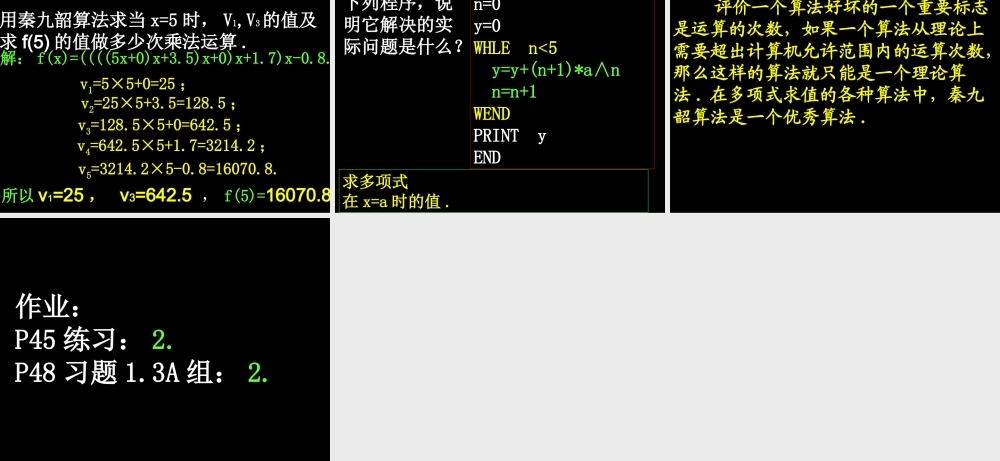
1.3 算法案例 第二课时 问题提出 1. 辗转相除法和更相减损术,是求两个正整数的最大公约数的优秀算法,我们将算法转化为程序后,就可以由计算机来执行运算,实现了古代数学与现代信息技术的完美结合 . 2. 对于求 n 次多项式的值,在我国古代数学中有一个优秀算法,即秦九韶算法,我们将对这个算法作些了解和探究 .[ 问题 1] 设计求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当 x=5 时的值的算法 , 并写出程序 .x=5f=2 * x^5-5 * x^4-4 * x^3+3 * x^2-6 *x+7PRINT fEND程序点评 : 上述算法一共做了 15 次乘法运算 ,5次加法运算 . 优点是简单 , 易懂 ; 缺点是不通用 ,不能解决任意多项多求值问题 , 而且计算效率不高 .知识探究 ( 一 ): 秦九韶算法的基本思想 思考 2: 在上述问题中,若先计算 x2 的值,然后依次计算 x2·x , (x2·x)·x ,((x2·x)·x)·x 的值,这样每次都可以利用上一次计算的结果,,那么一共做了多少次乘法运算和多少次加法运算? 9 次乘法运算, 5 次加法运算 . 第二种做法与第一种做法相比 , 乘法的运算次数减少了 , 因而能提高运算效率 . 而且对于计算机来说 ,做一次乘法所需的运算时间比做一次加法要长得多 ,因此第二种做法能更快地得到结果 .思考 3: 能否探索更好的算法 , 来解决任意多项式的求值问题 ?f(x)=2x5-5x4-4x3+3x2-6x+7=(2x4-5x3-4x2+3x-6)x+7=((2x3-5x2-4x+3)x-6)x+7=(((2x2-5x-4)x+3)x-6)x+7=((((2x-5)x-4)x+3)x-6)x+7v0=2v1=v0x-5=2×5-5=5v2=v1x-4=5×5-4=21v3=v2x+3=21×5+3=108v4=v3x-6=108×5-6=534v5=v4x+7=534×5+7=2677所以 , 当 x=5 时 , 多项式的值是 2677.这种求多项式值的方法就叫秦九韶算法 .5 次乘法运算, 5 次加法运算 . 思考 4: 利用最后一种算法求多项式f(x)=anxn+an-1xn-1+…+a1x+a0 的值,这个多项式应写成哪种形式?f(x)=anxn+an-1xn-1+…+a1x+a0 =(anxn-1+an-1xn-2+…+a2x+a1)x+a0=((anxn-2+an-1xn-3+…+a2)x+a1)x+a0 =…=(…((anx+an-1)x+an-2)x+…+a1)x+a0.思考 4: 对于 f(x)=(…((anx+an-1)x+ an-2)x+…+a1)x+a0 ,由内向外逐层计算一次多项式的值,其算法步骤如何? 第一步,计算 v1=anx+an-1. 第二步,计算 v2=v1x+an-2.第三步,计算 v3=v2x+an-3. …第 n 步,计算 vn=vn-1x+a0.思考 5: 上述求多项式 f(x)=anxn+an-1xn-1+…+a1x+a0 的值的方法称为秦九韶算法,...