江苏地区高二数学定积分的应用课件 苏教版 课件VIP免费

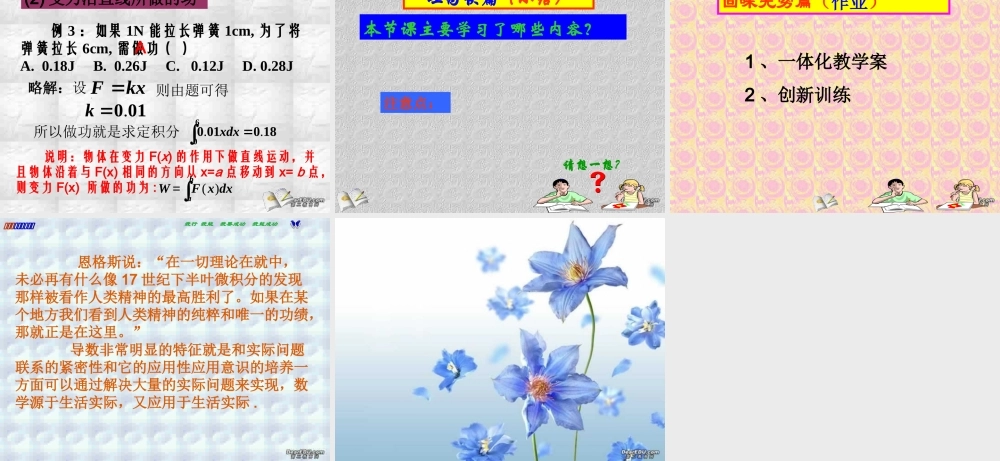
问题情境（复习引入）1 、求曲边梯形的思想方法是什么？2 、定积分的几何意义是什么？3 、微积分基本定理是什么？ 课课课课课课课课课课课课课课课课课课我行 我能 我要成功 我能成功例题研究 （一）利用定积分求平面图形的面积 例 1 、求曲线 与直线 x 轴所围成的图形面积。 ]32,0[sinxxy ,32,0xx2332320oxxdxS|cossin＝ 略解：根据定积分的几何意义所求面积为 课课课课课课课课课课课课课课课课课课我行 我能 我要成功 我能成功变式引申： 1 、求直线 与抛物线 所围成的图形面积。32 xy2xy 332|)33)323132231xxxdxxxS（－＋（＝32 xy 略解：如图直线与抛物线2xy 的交点坐标为（－ 1 ， 1）和（ 3 ， 9 ），则课课课课课课课课课课课课课课课课课课我行 我能 我要成功 我能成功变式引申2 、求由抛物线342xxy 及其在点M （ 0 ，－ 3 ）和 N （ 3 ， 0 ）处的两条切线所围成的图形的面积。 xyoy= － x2+4x-3略解：42xy /则在 M 、 N 点处的切线方程分别为、34 xy62xy则所求图形的面积为49)]34()62[()]34()34[(22303232＝＝dxxxxdxxxxS课课课课课课课课课课课课课课课课课课我行 我能 我要成功 我能成功变式引申3 、求曲线xy2log与曲线)(logxy42以及 x轴所围成的图形面积。 略解：如图由xy2log得yyfx2)(当)()(),(yfygy时，10则所求图形的面积为dydyyfygSy1010224)()()(【＝eeyy210224224log|)log（由)(logxy42yygx24 )(得课课课课课课课课课课课课课课课课课课我行 我能 我要成功 我能成功变式引申4 、在曲线)0(2xxy 上的某点 A 处作一切线使之与曲线以及 x 轴所围成的面积为121.试求：切点 A 的坐标以及切线方程 . x yOy=x2ABC略解：如图由题可设切点坐标为),200 xx（xy2/则切线方程为2002xxxy 轴的交点坐标为x切线与),(020x 则由题可知有1211223022002202000xdxxxxxdxxSxxx)(10  x所以切点坐标与切线方程分别为12),1,1(A xy课课课课课课课课课课课课课课课课课课我行 我能 我要成功 我能成功 （ 1 ）画图 , 并将图形分割为若干个曲边梯形； （ 2 ）对每个曲边梯形确定其存在的范围 , 从而确定积分的上、下限； （ 3 ）确定被积函数；...