高中数学 212 椭圆的简单几何性质课件 新人教A版选修1-1 课件VIP免费

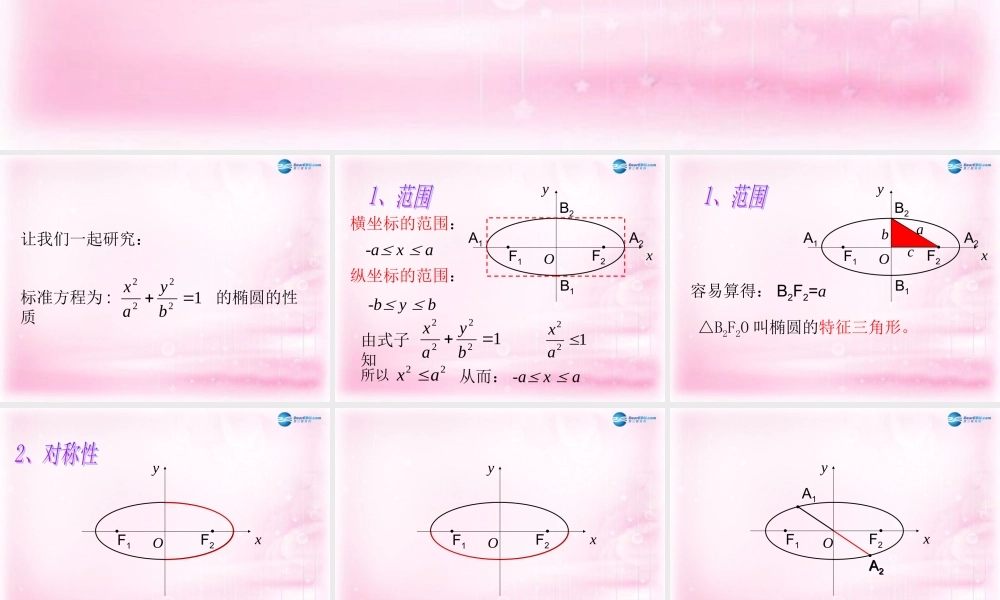
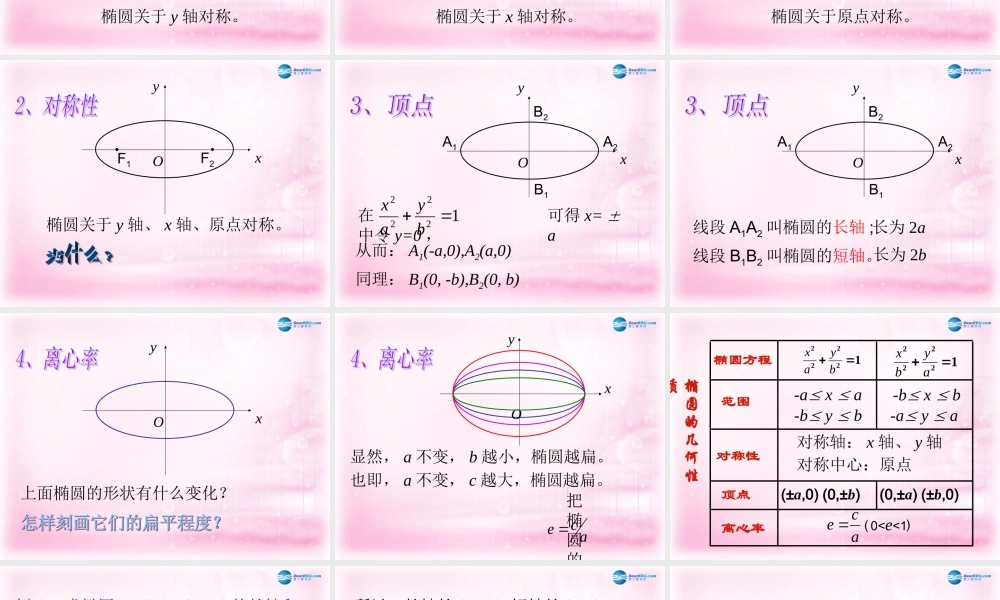
标准方程为 : 的椭圆的性质12222byax让我们一起研究： F2F1OB2B1A1A2xy横坐标的范围：纵坐标的范围：-a x  a-b y  b122ax所以 22ax 由式子 知12222byax从而： -a x  a aF2F1OB2B1A1A2xycb容易算得： B2F2=a △B2F2O 叫椭圆的特征三角形。 F2F1Oxy椭圆关于 y 轴对称。 F2F1Oxy椭圆关于 x 轴对称。 A2A1A2F2F1Oxy椭圆关于原点对称。 F2F1Oxy椭圆关于 y 轴、 x 轴、原点对称。 OB2B1A1A2xy可得 x=  a在 中令 y=0 ，12222byax从而： A1(-a,0),A2(a,0)同理： B1(0, -b),B2(0, b) OB2B1A1A2xy线段 A1A2 叫椭圆的长轴 ;线段 B1B2 叫椭圆的短轴。长为 2a长为 2b 上面椭圆的形状有什么变化？Oxy Oxy显然， a 不变， b 越小，椭圆越扁。也即， a 不变， c 越大，椭圆越扁。把椭圆的焦距与长轴长的比 称为椭圆的离心率，用e表示，即acace  )(012222babyax)(012222baaybx(±a,0) (0,±b)(0,±a) (±b,0)ace  0