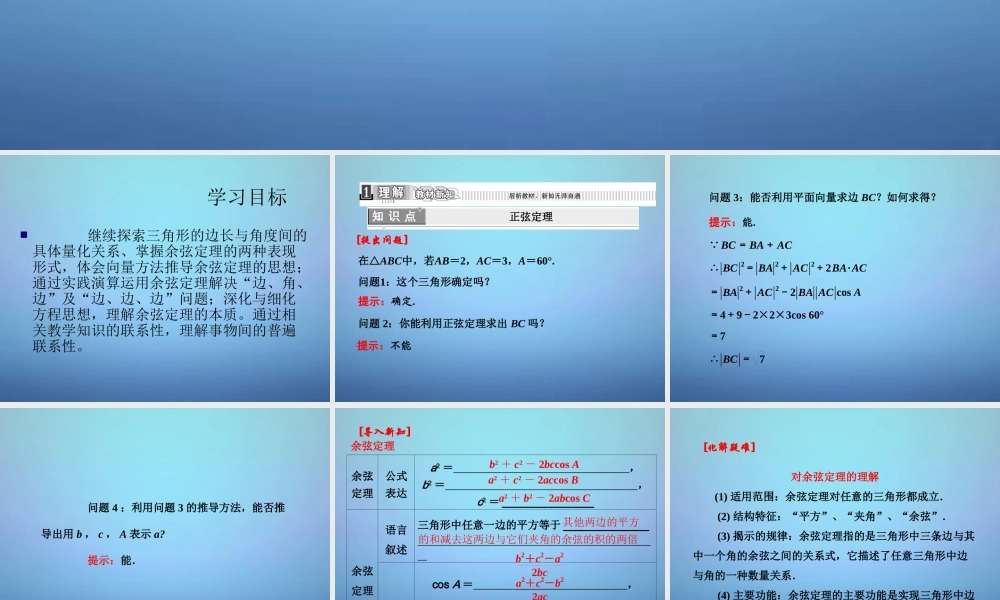
余弦定理余弦定理余弦定理余弦定理高中数学高一年级必修五第一章 第 1.1.2 节高中数学高一年级必修五第一章 第 1.1.2 节 学习目标 继续探索三角形的边长与角度间的具体量化关系、掌握余弦定理的两种表现形式,体会向量方法推导余弦定理的思想;通过实践演算运用余弦定理解决“边、角、边”及“边、边、边”问题;深化与细化方程思想,理解余弦定理的本质。通过相关教学知识的联系性,理解事物间的普遍联系性。正弦定理 在△ABC中,若AB=2,AC=3,A=60°. 问题1:这个三角形确定吗? 提示:确定. 问题 2:你能利用正弦定理求出 BC 吗? 提示:不能 [提出问题] 问题 3:能否利用平面向量求边 BC?如何求得? 提示:能. BC�=BA�+AC� ∴ BC�2= BA�2+ AC�2+2BA�·AC� = BA�2+ AC�2-2 BA�AC�cos A =4+9-2×2×3cos 60° =7 ∴ BC�= 7 问题 4 :利用问题 3 的推导方法,能否推导出用 b , c , A 表示 a? 提示:能.[导入新知] 余弦定理余弦定理公式表达a2 = ,b2 = ,c2 = _______________余弦定理语言叙述三角形中任意一边的平方等于 ___________________________________________________________________推论cos A = ,cos B = ,cos C = ____________ b2 + c2 - 2bccos Aa2 + c2 - 2accos Ba2 + b2 - 2abcos C其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍b2+c2-a22bc a2+c2-b22ac a2+b2-c22ab [化解疑难] 对余弦定理的理解 (1) 适用范围:余弦定理对任意的三角形都成立. (2) 结构特征:“平方”、“夹角”、“余弦”. (3) 揭示的规律:余弦定理指的是三角形中三条边与其中一个角的余弦之间的关系式,它描述了任意三角形中边与角的一种数量关系. (4) 主要功能:余弦定理的主要功能是实现三角形中边角关系的互化.已知三角形的三边解三角形[例 1] 在△ABC 中,若 a∶b∶c=1∶ 3∶2,求 A,B,C. [解] 由于 a∶b∶c=1∶ 3∶2, 可设 a=x,b= 3x,c=2x. 由 余 弦 定 理 的 推 论 , 得 cos A = b2+c2-a22bc=3x2+4x2-x22× 3x×2x = 32 ,故 A=30°. 同理可求得 cos B=12,cos C=0,所以 B=60°,C=90°. [ 类题通法 ]已知三角形的三边解三角形的方法 (1) 先利用余弦定理求出一个角的余弦,从而求出第一个角;再利用...