福建省福鼎市高一数学(余弦函数图像与性质)课件VIP免费

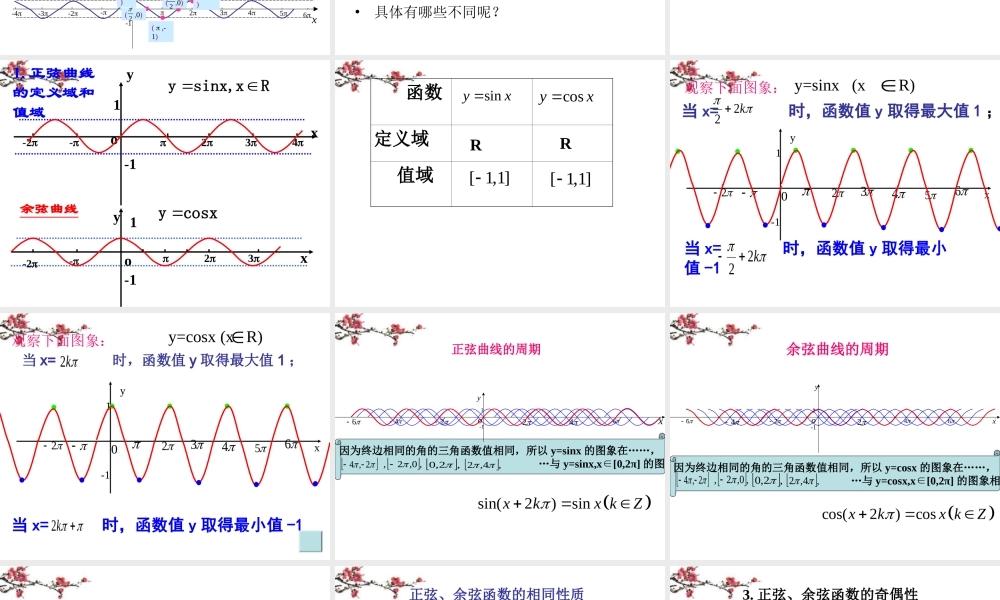
余弦函数的图象与性质X正弦函数的图象•描点法•几何法•五点法（关键点）思考： 余弦函数怎么画呢？余弦函数的图像• 描点法• 几何法• 五点法思考：还有其他的方法吗？Rx , cosxy-2-o23x-11y提示：由已知到未知？作余弦函数 y=cosx (x∈R) 的图象 思考：如何将余弦函数用诱导公式写成正弦函数？x)cos(cosxyx)](2πsin[x)2πsin( 注：余弦曲线的图象可以通过将正弦曲线向左平移 个单位长度而得到。余弦函数的图象叫做余弦曲线。2πx6yo--12345-2-3-41 正弦、余弦函数的图象 余弦函数的图象 正弦函数的图象 x6yo--12345-2-3-41y=cosx=sin(x+ ), xR2余弦曲线(0,1)( ,0)2(  ,-1)( ,0)23( 2 ,1)正弦曲线形状完全一样只是位置不同正弦函数的性质•我们已经学习了正弦函数的性质，能不能类比学习余弦函数的性质呢？1. 定义域2. 值域3. 周期性4. 单调性5. 奇偶性6. 对称性•具体有哪些不同呢？余弦函数的性质•我们从下面几个方面考虑：1. 定义域和值域2. 周期性3. 单调性4. 奇偶性5. 对称性xyo1-1-2-234Rxsinx,y1. 正弦曲线的定义域和值域Rx , cosxy-2-o23x-11y余弦曲线 函数定义域 值域sinyxcosyx[ 1,1][ 1,1]RRyx2346021-15 y=sinx (x R) 当 x= 时，函数值 y 取得最大值 1 ；k22当 x= 时，函数值 y 取得最小值 -1k22观察下面图象：yx2346021-15 y=cosx (x R) 当 x= 时，函数值 y 取得最大值 1 ；k2当 x= 时，函数值 y 取得最小值 -1 k2观察下面图象：因为终边相同的角的三角函数值相同，所以 y=sinx 的图象在……， …与 y=sinx,x[0,2π]∈的图象相同2,4,0,2,,2,0,4,2正弦曲线的周期xy---------1-12o46246sin(2)sinxkx kZ因为终边相同的角的三角函数值相同，所以 y=cosx 的图象在……， …与 y=cosx,x[0,2π]∈的图象相同 2,4 ,0,2,,2,0 ,4,2余弦曲线的周期2o46246xy---------1-1 cos(2)cosxkx kZ 由此可知，2 ,4 ,, 2 , 4 ,2(,0)kkZ k2都是这两个函数的周期。是它的周期，最小正周期...