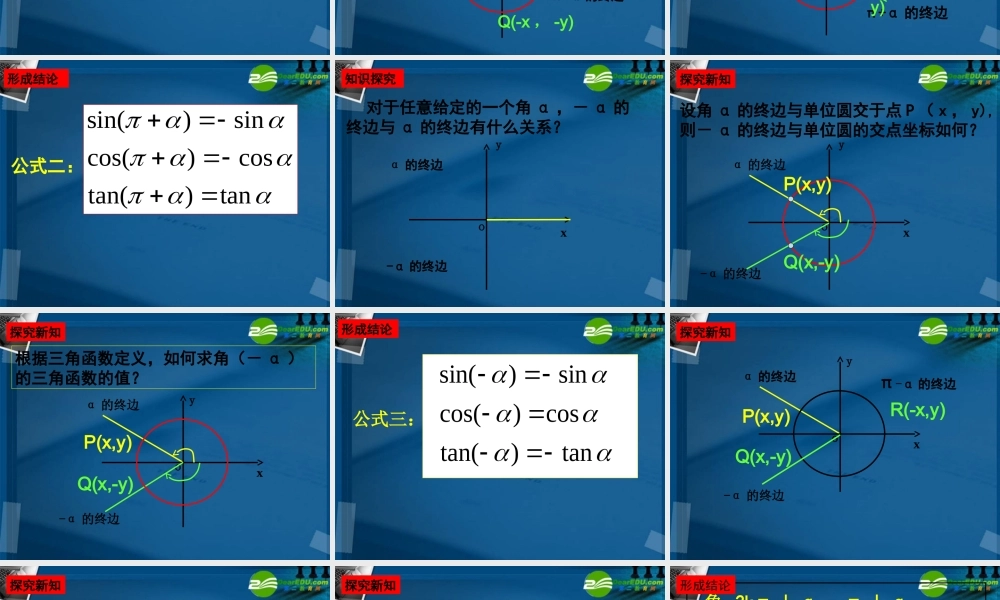
高一数学必修 4 第一章同名三角函数的诱导公式( 1 )知识回顾1. 任意角 α 的正弦、余弦、正切是怎样 定义的?α 的终边P(x , y)Oxysiny cosx tan(0)y xx 2. 2kπ + α ( k∈Z )与 α 的三角函数之间 的关系是什么?(即公式一)公式一: sin(2)sinkcos(2)cosktan(2)tankkZ( )3. 求 sin 和 cos930° 的值 .296知识回顾 利用公式一,可将任意角的三角函数值,转化为 00 ~ 3600 范围内的三角函数值 .其中锐角的三角函数可以查表计算,而对于 900 ~ 3600 范围内的三角函数值,如何转化为锐角的三角函数值,是我们需要研究和解决的问题 .1.3 三角函数的诱导公式 第一课时同名三角函数的诱导公式α 的终边xyoπ+α 的终边对于任意给定的一个角 α ,角 π + α 的终边与角 α 的终边有什么关系?探究新知P(x , y)Q(-x , -y)求 sin ( π + α )、 cos ( π +α )、tan ( π + α )的值 .α 的 终边xyoπ+α 的终边P(x ,y)Q(-x , -y)探究新知 公式二: tan)tan(cos)cos(sin)sin(形成结论知识探究 对于任意给定的一个角 α ,- α 的终边与 α 的终边有什么关系? yα 的终边xo-α 的终边设角 α 的终边与单位圆交于点 P ( x , y),则- α 的终边与单位圆的交点坐标如何?yα 的终边xo-α 的终边P(x,y)Q(x,-y)探究新知根据三角函数定义,如何求角(- α )的三角函数的值?yα 的终边xo-α 的终边P(x,y)Q(x,-y)探究新知 公式三: tan)tan(cos)cos(sin)sin(形成结论-α 的终边yα 的终边xoP(x,y)R(-x,y)π-α 的终边Q(x,-y)探究新知 公式四: sin()sincos()costan()tan探究新知 公式一~公式四都叫做诱导公式它们分别反映了 2kπ + α , π +α ,- α , π - α ( k∈Z ),的三角函数与 α 的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗? 探究新知 角 2kπ + α , π + α ,-α ,π - α ( k∈Z )的三角函数值,等于 α 的同名函数值,再放上原函数的象限符号 . 公式一~公式四都是同名三角函数 函数同名,象限定号形成结论利用诱导公式一~公式四,怎样求任意角的三...