高中数学(微积分基本定理)课件1 新人教A版选修2-2 课件VIP免费

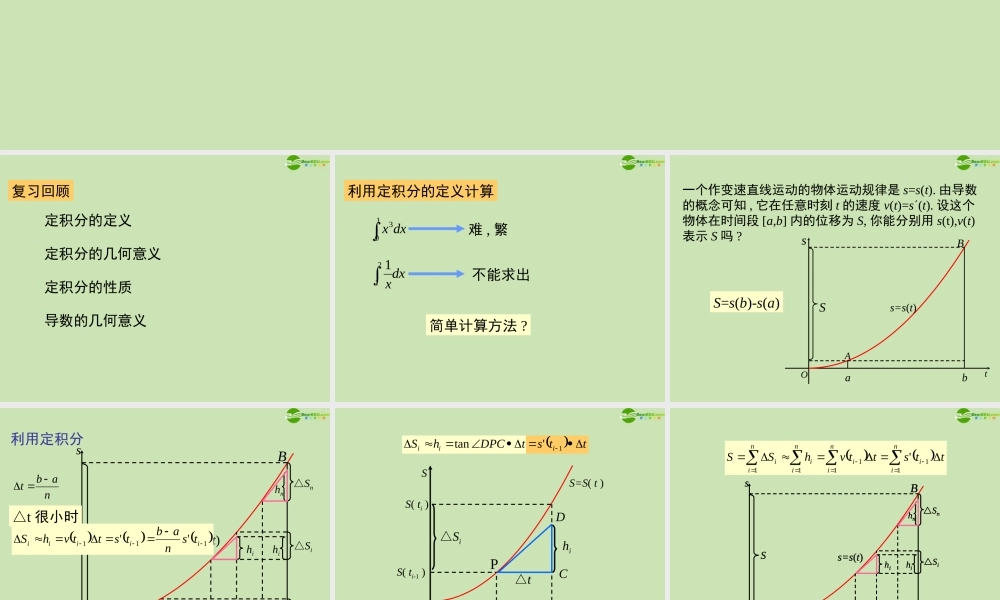
复习回顾定积分的定义定积分的几何意义定积分的性质导数的几何意义 dxx103dxx211难 , 繁不能求出利用定积分的定义计算简单计算方法 ? 一个作变速直线运动的物体运动规律是 s=s(t). 由导数的概念可知 , 它在任意时刻 t 的速度 v(t)=s(t). 设这个物体在时间段 [a,b] 内的位移为 S, 你能分别用 s(t),v(t)表示 S 吗 ?SOtss=s(t)baABS=s(b)-s(a) SOsts=s(t)△Sn△Si△S1h1h1hihihnAa(t0)t0ti-1titn-1 b(tn)Bnabt利用定积分111''iiiiitsnabtsttvhS△t 很小时 tDPChSiitanSS=S( t )S( ti )S( ti-1 )ttiti-1ODC△Si△thiPttsi 1' niiniiniiniittsttvhSS111111'SOsts=s(t)△Sn△Si△S1h1h1hihihnAa(t0)t0ti-1titn-1 b(tn)BSOstOsts=s(t)s=s(t)△Sn△Si△S1△Sn△Si△S1h1h1h1h1h1hihihihihihnhnAa(t0)t0ti-1titn-1 b(tn)BAa(t0)t0ti-1titn-1 b(tn)a(t0)t0ti-1titn-1 b(tn)B n∞△t0S niitts11'niintvnabS11limttsnabniin11'lim badttv badtts'    asbsdttsdttvSbaba' 微积分基本定理又叫牛顿－莱布尼兹公式如果 f (x) 是区间 [a,b] 上连续函数 , 并且 F(x)=f (x), 那么   baaFbFdxxf  baFaFbF 记   babaaFbFFdxxf| 例 1 计算下列定积分 : 21;11dxx 312;122dxxx  xfx F'找满足关键 xx1'ln 1解2ln1ln2ln|ln12121xdxx 例 1 计算下列定积分 : 21;11dxx 312;122dxxx解  ,1'1 ,2' 222xxxx31231312 1 212dxxdxxdxxx31312|1|xx1311922 例 2 计算下列定积分 :2020sin ,sin ,sinxdxxdxxdx(-cosx)=sinx解 ;20coscos|cos sin00xdxx212y=sinxxy  .00cos2cos|cos sin2020xdxx ;2cos2cos|cos sin22xdxx12y=sinxxy212y=sinxxy2 堂上练习计算下列定积分        ;1234 ;13;22;413122150250dxxxdxxdxxxxdx     .sin 8 ;cos 7;16 ;150021221xdxxdxdxxdxxx堂上练习计算下列定积分 微积分的基本定理 ( 牛顿－莱布尼兹公式 )小结如果 f (x) 是区间 [a,b] 上连续函数 , 并且 F(x)=f (x), 那么   baaFbFdxxf 作业课本第 62 页习题 1.6A 组 题 1,2