高中数学 1.2 余弦定理课件2 苏教版必修5 课件VIP免费

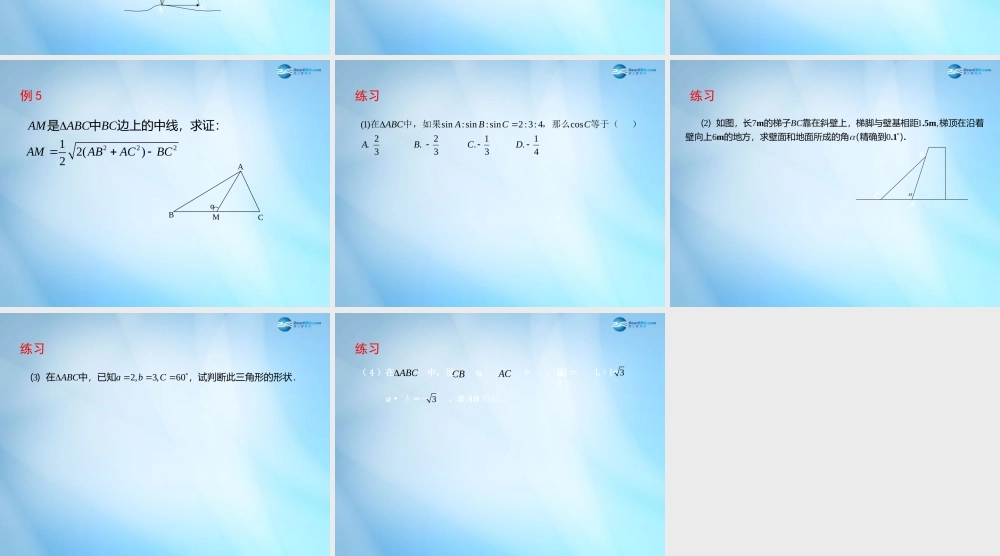
复习余弦定理：Abccbacos2222Baccabcos2222Cabbaccos2222bcacbA2cos222cabacB2cos222abcbaC2cos222一、二、探讨：实际生活中有哪些问题可以利用余弦定理来解决？例 1182m,126m,631mABCCACBACBAB ， 两地之间隔着一个水塘，先选择另一点 ，测得，求 ， 两地之间的距离（精确到）．A BC例 2 在长江某渡口处，江水以 5km/h 的速度向东流．一渡船在江南岸的 A 码头出发，预定要在 0.1h 后到达江北岸 B 码头．设 为正北方向，已知 B 码头在 A 码头的北偏东 ，并与 A 码头相距1.2km ．该渡船应按什么方向航行？速度是多少（角度精确到 ，速度精确到 0.1km/h)?AN�150.1ACBND例 3sin2sincosABCABC在中，已知，试判断该三角形的形状．例 4coscoscosABCaAbBcCABC在中，已知，试判断的形状．例 522212()2AMABCBCAMABACBC是中边上的中线，求证：αMCBA练习41.31.32.32.cos4:3:2sin:sin:sin)1(DCBACCBAABC）等于（，那么中，如果在练习271,60m.5mm.1 .BC（ ）如图，长的梯子靠在斜壁上，梯脚与壁基相距梯顶在沿着壁向上的地方，求壁面和地面所成的角 （精确到）ABC练习32,3,60ABCabC（ ）在中，已知，试判断此三角形的形状．练习ABCCB�AC�（ 4 ）在 中，设 = ， = ，且 ， aｂ|a| ＝2| ｂ |= 3a· ｂ＝－ ，求 AB 的长．3