高中数学 312 两角和与差的正弦、余弦、正切公式课件 新人教A版必修4 课件VIP免费

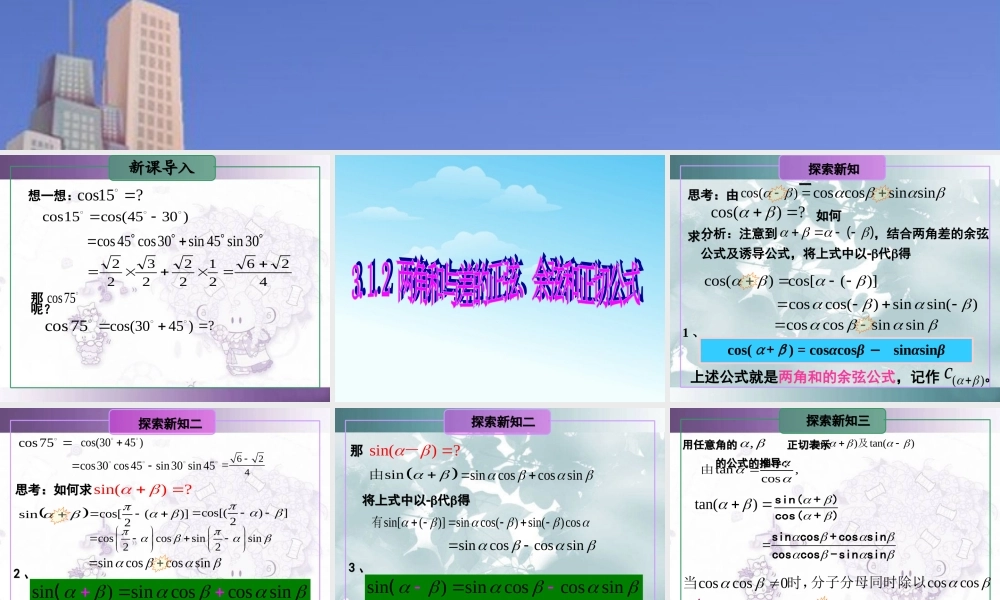
3.1.2 两角和与差的正弦、余弦、正切公式新课导入新课导入想一想：cos15?30sin45sin30cos45cos42621222322那 呢？cos75cos15cos(4530 )cos75 cos(3045 )?分析：注意到 ，结合两角差的余弦公式及诱导公式，将上式中以代得 （）cos()cos[()] coscos()sinsin()coscossinsin上述公式就是两角和的余弦公式，记作 。()c  cos cossin sincos()cos()?思考：由 如何求 : 思考：由 如何求 : 探索新知一 探索新知一1 、cos(α+β) = cosαcosβ － sinαsinβ 探索新知二 探索新知二sin()?思考：如何求思考：如何求 sincos[()]2coscossinsin22sincoscossincos[()]2cos75 cos(3045 )cos30 cos45sin30 sin 45624sin)sincoscossin(2 、2 、()S  上述公式就是两角和的正弦公式，记作 。 探索新知二 探索新知二sin()? －那那()S  上述公式就是两角差的正弦公式，记作 。sin)sincoscossin(3 、3 、sincoscossinsin[()]sincos()sin()cos 有将上式中以代得将上式中以代得sin 由sincoscossin 探索新知三 探索新知三用任意角的 正切表示 的公式的推导 :用任意角的 正切表示 的公式的推导 :, tan()tan()及sin cos+ cos sincos cos-sin sinsin(+)cos(+)coscos0 当时，coscos分子分母同时除以tan()tan+ tantan(+)= 1- tan tan() 记：+T4 、4 、sintan,cos由将上式两角和的正切公式以代得 tantan()tan[()]1tantan()  tan- tan= 1+ tan tan 探索新知三 探索新知三() 记-Ttan- tantan(-)=1+ tan tan5 、5 、注意： 1 、必须在定义域范围内使用上述公式。 2 、注意公式的结构，尤其是符号。即： tan ， tan ， tan(±) 只要有一个不存在就不能使用这个公式。tan()? －那那33sin,sin...