高中数学 3.1.1两角差的余弦公式课件 新人教A版必修4VIP免费

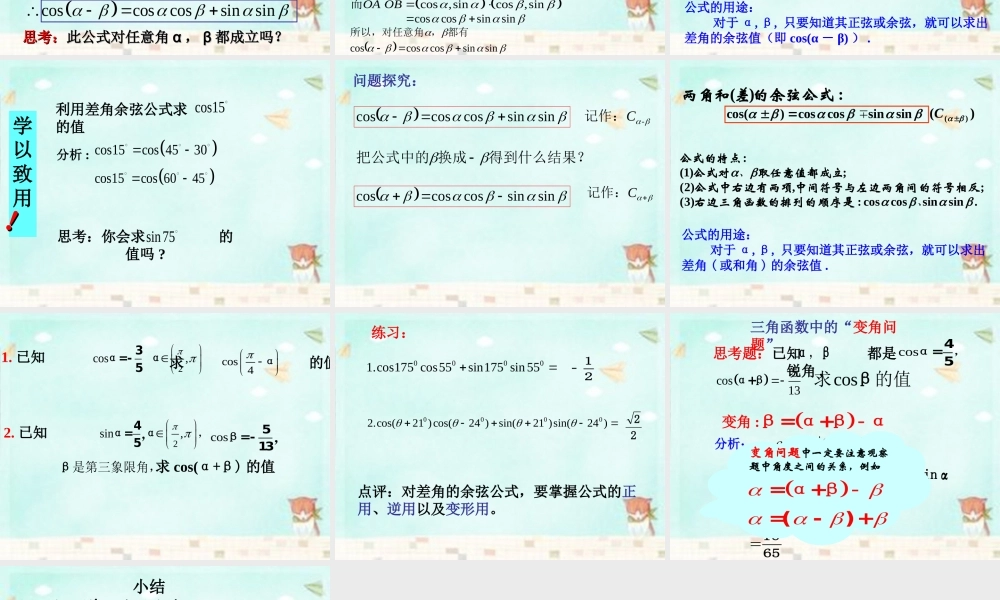
3.1.1 两角差的余弦公式复习回顾：任意角的三角函数定义 设 是一个任意角，它的终边与单位圆交于点),(yxP 那么 : （ 1 ） 叫做 的正弦，记作 ，即 ；ysinysin （ 2 ） 叫做 的余弦，记作 ，即 ； cosxxcos（ 3 ） 叫做 的正切，记作 ，即 。 xytanxytan 所以，正弦，余弦，正切都是以角为自变量，以单位圆上点的坐标或坐标的比值为函数值的函数，我们将他们称为三角函数 .0,1AOyxyxP , ﹒)0(xα 的终边α 的终边不用计算器，求 的值 . 1. 15 ° 能否写成两个特殊角的和或差的形式 ? 2. cos (450 - 30 0) 能否用 45 ° 和 30 ° 的角的 三角函数来表示 ? 如果能 , 那么一般地 cos(α-β) 能否用 α 、 β 的角的三角函数来表示 ?cos375cos375cos375cos 36015cos15 解：问题：3045cos15cos4560cos15cos你认为会是cos(α-β)=cosα-cosβ 吗 ?问题探究如何用任意角 α 与 β 的三角函数来表示 cos(α-β) ？主要方法：1. 利用单位圆的三角函数线（课后阅读教材 125 页，作为了解）2. 利用向量知识（重点掌握）αABcos,sinOB� 下面我们用向量知识探究：Ｏxyαββ如图：单位圆中cos ,sin,OA�cosOA OBOA OB�cos. cos,sincos,sinOA OB�而coscossinsincoscoscossinsin思考：思考：此公式对任意角此公式对任意角 αα ，， ββ 都成立吗？都成立吗？  sin,cos sin,cosβ 终边α 终边BAOXYBAOXYα 终边β 终边的夹角为与设OBOA.2--22kkk即，或在任意角范围下，coscos2coscosk由,0sinsincoscoscos都有，所以，对任意角 cos,sincos,sinOA OB�而coscossinsinOBOA.sinsincoscos:)3(;,)2(;)1(:、、顺序是右边三角函数的排列的的符号相反中间符号与左边两角间公式中右边有两项取任意值都成立公式对公式的特点两角差的余弦公式sinsincoscoscos的余弦公式。简记为之间的关系。称为差角的余弦...