高中数学 函数y=Asinwxφ的图象1课件 新人教A版必修1 课件VIP免费

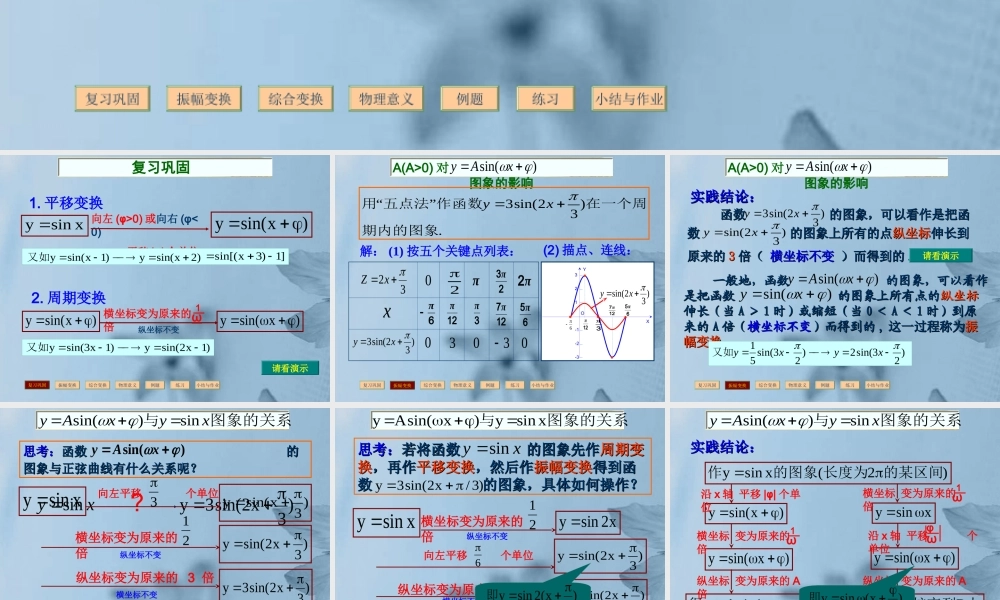
复习巩固振幅变换综合变换物理意义例题练习1.5 函数 的图象)sin( xAy第 2 课时小结与作业纵坐标不变横坐标变为原来的 倍ω1向左 (φ>0) 或向右 (φ<0) 平移 |φ| 个单位)2xsin(y)1xsin(y又如复习巩固振幅变换综合变换物理意义例题练习复习巩固复习巩固)xsin(y)xsin(y)xsin(yxsiny 1. 平移变换2. 周期变换小结与作业]1)3xsin[()1x2sin(y)1x3sin(y又如请看演示复习巩固振幅变换综合变换物理意义例题练习振幅变换A(A>0) 对 图象的影响)sin( xAy.)32sin(3”“期内的图象在一个周作函数五点法用xy解： (1) 按五个关键点列表：(2) 描点、连线：127π3π12π65π)32sin(3xy32 xZxπ2π223π6π003030OXY321-1-2-3.....127π3π12π65π6小结与作业)32sin(xy复习巩固振幅变换综合变换物理意义例题练习振幅变换A(A>0) 对 图象的影响)sin( xAy 函数 的图象，可以看作是把函函数 的图象，可以看作是把函数 的图象上所有的点数 的图象上所有的点纵坐标纵坐标伸长到伸长到原来的原来的 33 倍（ 倍（ 横坐标不变横坐标不变 ）而得到的 ）而得到的 .. )32sin(xy)32sin(3xy实践结论：实践结论： 一般地，函数 的图象，可以看作一般地，函数 的图象，可以看作是把函数 的图象上所有点的是把函数 的图象上所有点的纵坐标纵坐标伸长（当伸长（当 AA ＞＞ 11 时）或缩短（当时）或缩短（当 00 ＜＜ AA ＜＜ 11 时）到原时）到原来的来的 AA 倍（倍（横坐标不变横坐标不变）而得到的）而得到的 ,, 这一过程称为这一过程称为振振幅变换幅变换 ..)sin( xAy)sin( xy请看演示小结与作业)23sin(2)23sin(51xyxy又如复习巩固振幅变换综合变换物理意义例题练习综合变换图象的关系与xyxAysin)sin(思考：思考：函数 的函数 的图象与正弦曲线有什么关系呢？图象与正弦曲线有什么关系呢？ )sin( xAy)3x2sin(3yxysin?)3x2sin(y)3xsin(yxsiny )3x2sin(3y向左平移 个单位3 纵坐标不变横坐标变为原来的 倍21 横坐标不变纵坐标变为原来的 3 倍请看演示小结与作业复习巩固振幅变换综合变换物理意义例题练习综合变换图象的关系与xsiny)xsin(Ay思考：思考：若将函数 的图象先作若...