高中数学 143正切函数图像及性质教学课件 新人教A版必修4 课件VIP免费

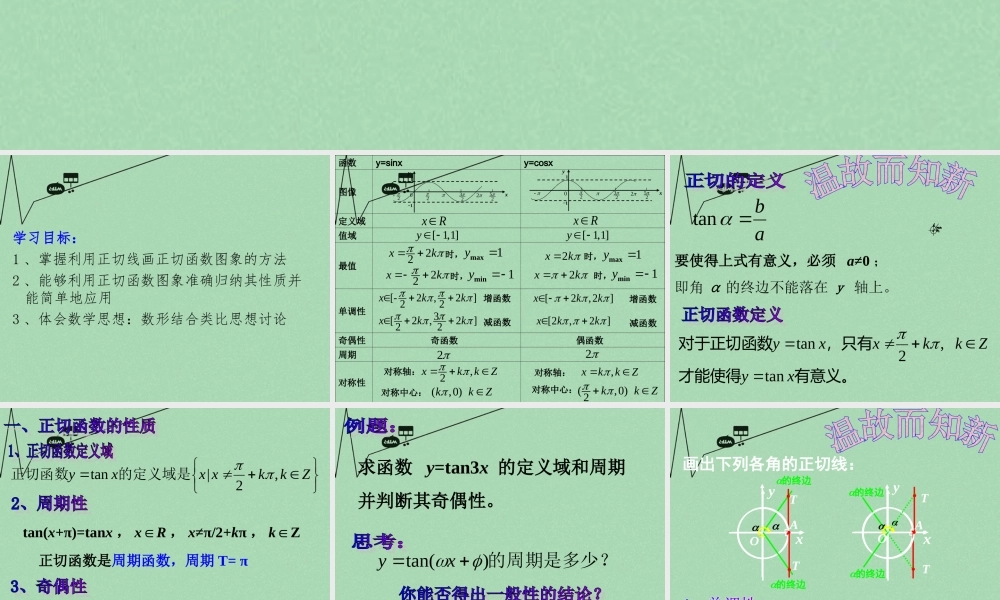
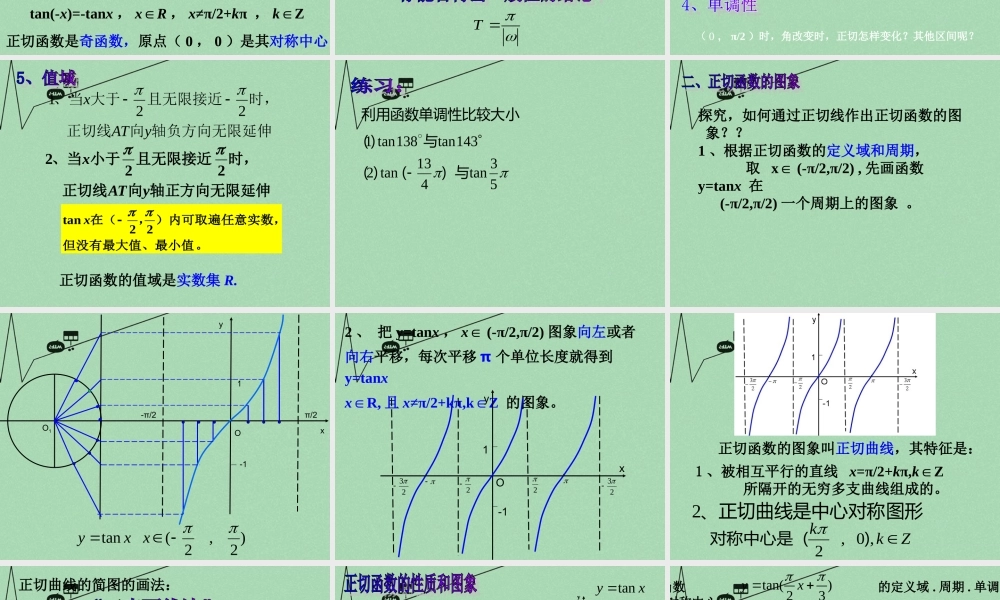
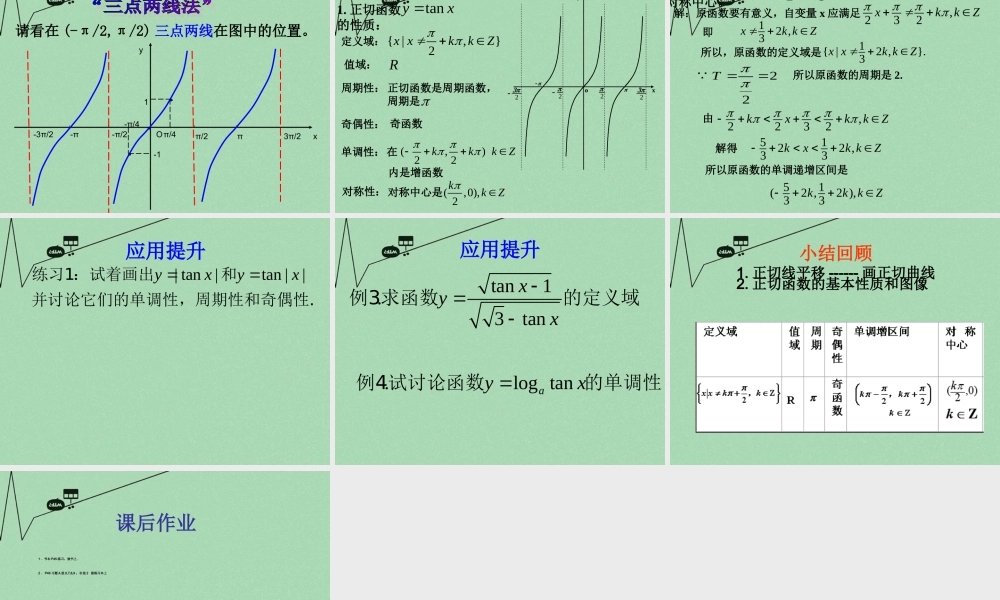
1.4.3学习目标：1 、掌握利用正切线画正切函数图象的方法2 、能够利用正切函数图象准确归纳其性质并能简单地应用3 、体会数学思想：数形结合类比思想讨论函数y=sinxy=cosx图像定义域值域最值单调性奇偶性周期对称性2522320xy21-1xRxR[ 1,1]y  [ 1,1]y  22xk时，1maxy22xk时，1miny2xk时，1maxy2xk 时，1miny[-2,2]22xkk增函数3[2,2]22xkk减函数[2,2]xkk 增函数[2,2]xkk 减函数2522320xy1-122对称轴：,2xkkZ对称中心： (,0) kkZ对称轴：,xkkZ对称中心：(,0)2 kkZ奇函数偶函数abtan要使得上式有意义，必须 a≠0 ；即角 α 的终边不能落在 y 轴上。有意义。才能使得，只有对于正切函数xyZkkxxytan,2tantan(x+π)=tanx ， x∈R ， x≠π/2+kπ ， k∈Z正切函数是周期函数，周期 T= πZkkxxxy,2|tan的定义域是正切函数tan(-x)=-tanx ， x∈R ， x≠π/2+kπ ， k∈Z正切函数是奇函数，原点（ 0 ， 0 ）是其对称中心求函数 y=tan3x 的定义域和周期并判断其奇偶性。的周期是多少？)tan( xyT画出下列各角的正切线： 的终边 的终边 的终边 y 的终边 y （ 0 ， π/2 ）时，角改变时，正切怎样变化？其他区间呢？轴负方向无限延伸向正切线时，且无限接近大于、当yATx221轴正方向无限延伸向正切线时，且无限接近小于、当yATx222。但没有最大值、最小值）内可取遍任意实数，，在（22tanx正切函数的值域是实数集 R.53tan413tan2143tan138tan1）与（）（与）（小利用函数单调性比较大探究，如何通过正切线作出正切函数的图 象？？1 、根据正切函数的定义域和周期， 取 x∈ (-π/2,π/2) , 先画函数y=tanx 在 (-π/2,π/2) 一个周期上的图象 。O11-1Oyx-π/2π/2)2,2(tanxxy2 、 把 y=tanx ， x∈ (-π/2,π/2) 图象向左或者向右平移，每次平移 π 个单位长度就得到y=tanx xR,∈且 x≠π/2+kπ,kZ∈ 的图象。Oyx1-1232223 正切函数的图象叫正切曲线，其特征是：1 、被相互平行的直线 x=π/2+kπ,k∈Z 所隔开的无穷多支曲线组成的。Zkk,0,2）对称中心是（ ...