高中数学 213 两直线的位置关系课件2 苏教版必修3 课件VIP免费

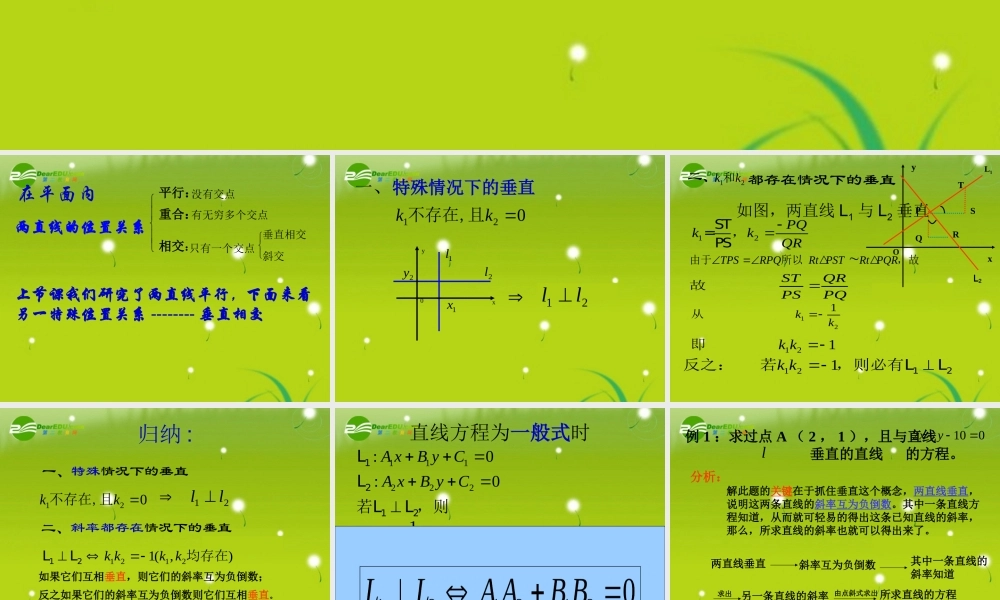
两直线的位置关系--- 两直线垂直 在平面内两直线的位置关系相交：平行：重合：斜交没有交点只有一个交点垂直相交有无穷多个交点上节课我们研究了两直线平行，下面来看另一特殊位置关系 -------- 垂直相交 一、特殊情况下的垂直21ll 120kk 不存在,且1l1x2l2yxy0 如图，两直线 L1 与 L2 垂直xyOL1PTSRQ二、都存在情况下的垂直12kk和12PQkkQRST=，PSTPSRPQRt PSTRt PQR由于所以 ，故STQRPSPQ故 121kk从 121k k 即 121k k 12反之： 若，则必有LLL2 归纳 :一、特殊情况下的垂直二、斜率都存在情况下的垂直12121( ,)k kk k12LL均存在21ll 120kk 不存在,且如果它们互相垂直，则它们的斜率互为负倒数；反之如果它们的斜率互为负倒数则它们互相垂直。 直线方程为一般式时111222:0:0A xB yCA xB yC1212LL若LL ，则121kk12（k，k 都存在）1212............(1)ABBA有缺陷吗？12120........(2)(1)A AB B与等价吗？ 例 1 ：求过点 A （ 2 ， 1 ），且与直线 垂直的直线 的方程。0102 yxl分析：解此题的关键在于抓住垂直这个概念，两直线垂直，说明这两条直线的斜率互为负倒数。其中一条直线方程知道，从而就可轻易的得出这条已知直线的斜率，那么，所求直线的斜率也就可以得出来了。两直线垂直斜率互为负倒数其中一条直线的斜率知道求出 另一条直线的斜率 由点斜式求出 所求直线的方程 例2(1）已知四点A(5, 3), B(10, 6), C(3, -4), D(-6, 11)求证：ABCD；两直线斜率存在吗 ?斜率存在时 , 怎样确定两直线垂直 ? 3 ,4112212例2(2）已知直线L的斜率k直线L 经过点A(3a, -2),B(0, a +1), 且LL ，求实数a的值.由两直线垂直 , 能得到什么结论 ?它与 a 有关系吗 ? 例 3 、已知三角形的顶点 A(2,4),B(1,-2),C(-2,3),求 BC 边上的高 AD 所在的直线方程 .xyo2-33-4xyoxyo2-33-4ABCD分析 :确定直线方程需要几个条件 ?已知什么 ?还缺什么 ?怎么解决 ? 一 . 判断下列两直线是否垂直 , 并说明理由 .(1)(2)(3)13:1 xyl831:2xyl643:1yxl734:2 yxl8:1xl3:2yl 二 . 基础练习：１、当 m 为 _____ 时，直线 mx-(3m-2)y=7 与 2x+my=1 互相垂直。２、已知直线 l1 :ax+by+2a=0 与直线 l2:(a-1)x+y+b=0 互相垂直，且直线 ...