高中数学 复数的运算三课件 新人教A版选修2-2 课件VIP免费

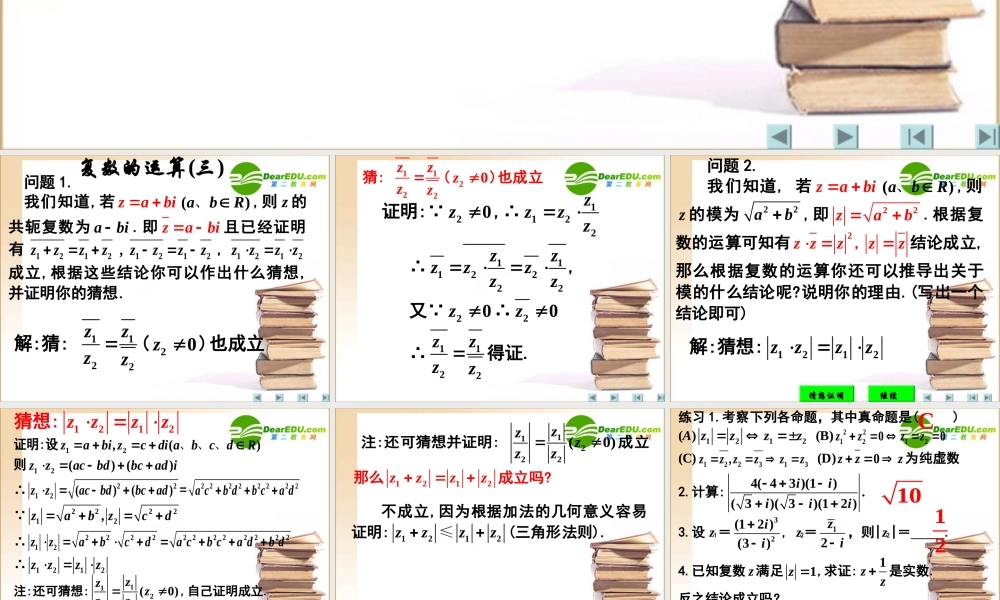
问题 2练习巩固问题 1问题 1 解答作业:自学《随堂通》106P至107P页内容. 复数的运算(三) 问题 1. 我们知道,若 zabi ()abR、,则 z 的共轭复数为 abi.即 zabi 且已经证明有12121212,zzzzzzzz,1212zzzz成立,根据这些结论你可以作出什么猜想,并证明你的猜想. 复数的运算(三) 解:猜: 1122zzzz(20z  )也成立 证明: 20z  ,∴1122zzzz ∴1112222zzzzzzz, 又 20z  ∴20z  ∴1122zzzz得证. 猜: 1122zzzz(20z  )也成立 问题 2. 我们知道, 若 zabi ()abR、,则z 的模为22ab,即22zab.根据复数的运算可知有2z zz , zz结论成立,那么根据复数的运算你还可以推导出关于模的什么结论呢?说明你的理由.(写出一个结论即可) 猜想证明继续解:猜想:1212zzzz 猜想:1212zzzz 证明:设12,()zabi zcdi abcdR  、 、 、 则12()()zzacbdbcad i ∴2212()()zzacbdbcad=22222222a cb db ca d 222212,zabzcd ∴22222222222212zzabcda cb ca db d ∴1212zzzz 注:还可猜想:11222(0)zzzzz,自己证明成立. 那么1212zzzz成立吗? 注:还可猜想并证明: 11222(0)zzzzz成立,那么1212zzzz成立吗? 不成立,因为根据加法的几何意义容易证明:1212zzzz≤(三角形法则). 练习 1.考察下列各命题，其中真命题是( ) (A)1212zzzz (B)22121200zzzz  (C)122313,zz zzzz (D)0zzz 为纯虚数 2.计算:4( 43 )(1).( 3)( 3)(12 )iiiii 3.设 z1＝32(12 )(3)ii, z2＝12zi，则|z2|＝ . 4.已知复数 z满足1z  ,求证:1zz是实数. 反之结论成立吗? 5.设 z为复数,且|| |1| 1|1|zzz ，求的值. 4 答案2 答案C 10 12 4.已知复数 z满足1z  ,求证:1zz是实数. 反之结论成立吗? 证明: 1z  ,∴1z z  ∴1z zzzzzzz   设()zabi abR 、,则1zbi  ∴2zzaR ∴1zz是实数. 5.设 z为复数,且|| |1| 1|1|zzz ，求的值. 解：设()zabi a bR ，1(1)| | |1| 1zabizz  ，且 22221(1)1abab2222120ababa 解方程组,...