高中数学函数y=Asinwxφ的图象课件 苏教版 必修4 课件VIP免费

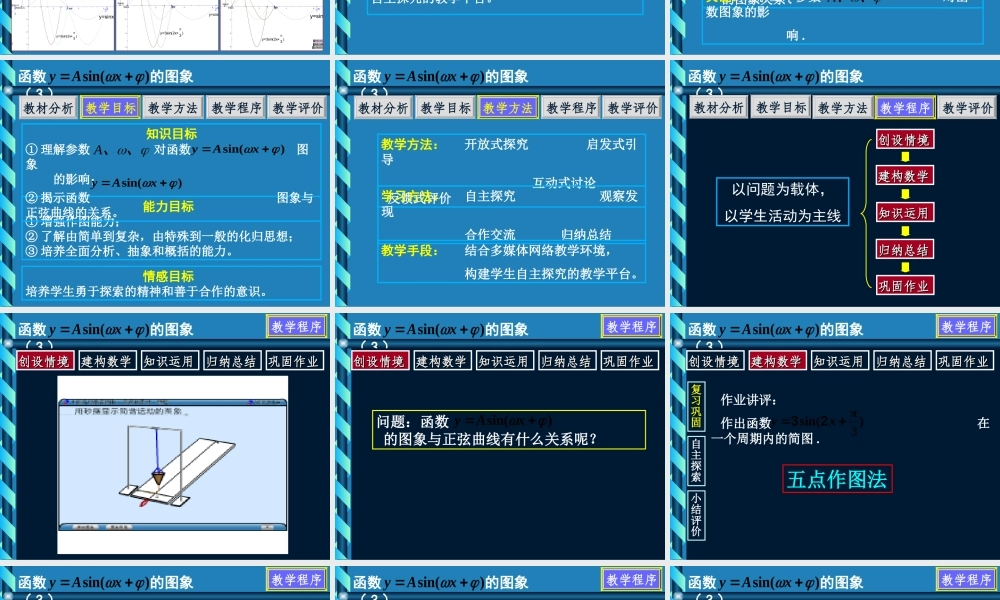
函数 的图象函数 的图象)sin( xAy 函数 的图象（ 3 ）)sin( xAy说课流程：教材分析教材分析教学目标教学目标教学程序教学程序教学评价教学评价教学方法教学方法 函数 的图象（ 3 ）)sin( xAy教材地位与作用 ① 它是函数图象伸缩、平移变换的特例； ② 它是初等数学函数图象变换的基础； ③ 它是历年高考的热点、难点问题。 教材分析教学目标教学方法教学程序 教学评价 ④ 它揭示正弦曲线得到函数 图象的一种思维过程。)sin( xAy 函数 的图象（ 3 ）)sin( xAy246321-1-2-3y=sinx-3y=3sin(2x+3 )23振幅平移点(pi/6)平移点(pi/3)振幅—平移—周期 函数 的图象（ 3 ）)sin( xAy振幅—平移—周期246321-1-2-3y=sinx-3y=3sin(2x+3 )23振幅平移点(pi/6)平移点(pi/3)平移—振幅—周期246321-1-2-3-3y=sinxy=3sin(2x+3 )23平移点振幅周期平移—周期—振幅246321-1-2-3-3y=sinxy=3sin(2x+3)2解：按五个关键点列表：平移点改变周期改变振幅振幅—周期—平移246321-1-2-3y=sinx-3y=3sin(2x+3 )23y=3sin(2x+(pi/3))振幅周期平移点(pi/3)平移点(pi/6)周期—振幅—平移321-1-2-3246y=3sin(2x+3 )y=sinx323平移点周期振幅平移点2周期—平移—振幅321-1-2-3246y=3sin(2x+3)y=sinx32y=3sin(2x+(pi/3))隐藏 关键点隐藏 坐标系平移点周期平移点2振幅振幅振幅 函数 的图象（ 3 ）)sin( xAy教材处理方法 精心设计制作教学课件，直观形象地展示变换过程。化抽象为具体，由静到动，使学生 真实体验“变”的过程。 结合多媒体网络教学环境，构建学生自主探究的教学平台。教材分析教学目标教学方法教学程序 教学评价 函数 的图象（ 3 ）)sin( xAy重点：由正弦曲线变换得到函数 图象 .)sin( xAy难点：当 时，函数 与 的图象关系 .1ω)sin(11φxωAy)sin(22φxωAy教材分析教学目标教学方法教学程序 教学评价A关键：理解三个参数 对函数图象的影 响 .、、A 函数 的图象（ 3 ）)sin( xAy能力目标 ① 增强作图能力；② 了解由简单到复杂，由特殊到一般的化归思想；③ 培养全面分析、抽象和概括的能力。教材分析教学目标教学方法教学程序 教学评价情感目标 培养学生勇于探索的精神和善于合作的意识。知识目标① 理解参数...