高二数学 定积分的概念 求曲边梯形的面积课件VIP免费

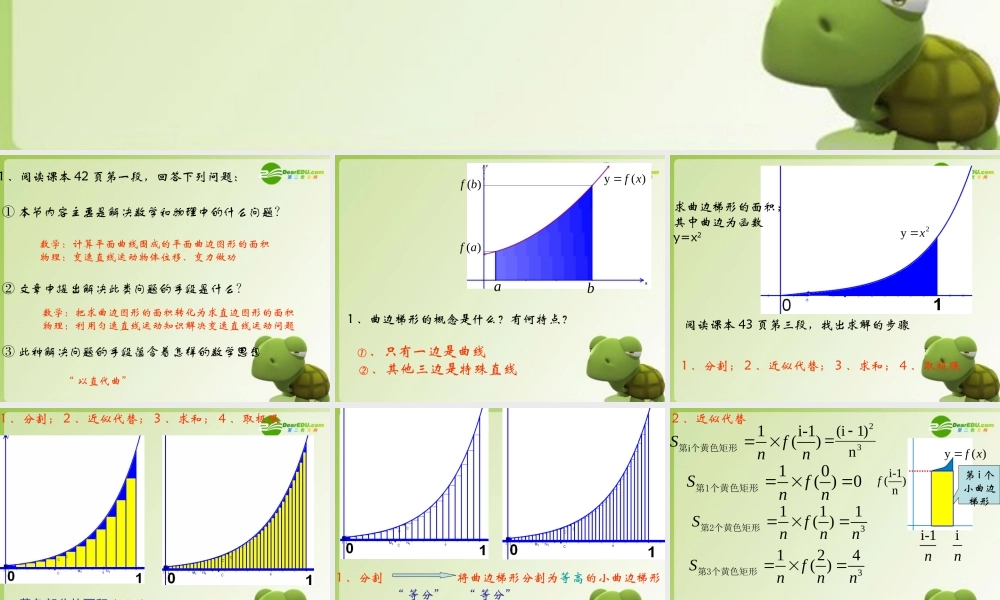
----------- 求曲边梯形的面积 1 、阅读课本 42 页第一段，回答下列问题：① 本节内容主要是解决数学和物理中的什么问题？② 文章中提出解决此类问题的手段是什么？数学：把求曲边图形的面积转化为求直边图形的面积物理：利用匀速直线运动知识解决变速直线运动问题数学：计算平面曲线围成的平面曲边图形的面积物理：变速直线运动物体位移、变力做功③ 此种解决问题的手段蕴含着怎样的数学思想“ 以直代曲” a)(afb)(bf)(yxf1 、曲边梯形的概念是什么？有何特点？ ① 、只有一边是曲线 ② 、其他三边是特殊直线 2yx求曲边梯形的面积；其中曲边为函数y=x2阅读课本 43 页第三段，找出求解的步骤1 、分割； 2 、近似代替； 3 、求和； 4 、取极限 1 、分割； 2 、近似代替； 3 、求和； 4 、取极限用黄色部分的面积来代替曲边梯形的面积，当曲边梯形分割的越细，蓝色部分面积就越小，就越接近曲边梯形的面积 1 、分割将曲边梯形分割为等高的小曲边梯形分割梯形分割 x 轴分割定义域“ 等分”“ 等分”]1,1[];......;3,2[];2,1[];1,0[nnnnnnn“ 等分”区间长度：n1 i-1n)(yxfini1i-1()Sfnn 第 个黄色矩形i-1()nf10( )0Sfnn 第1个黄色矩形3111( )Sfnnn 第2个黄色矩形3124( )Sfnnn 第3个黄色矩形231n-1(n-1)()Sfnnn 第n个黄色矩形2 、近似代替第 i 个小曲边梯形32n)1i(  S黄色部分3 、求和12n...SSS第 个黄色矩形第 个黄色矩形第 个黄色矩形3222n)1n(...3213232323232n1)-(n...n1)-(i...n2n1n0 S曲边梯形31 (1)[(1) 1][2(1) 1]6limnnnnn S曲边梯形4 、取极限S黄色部分limnS 黄色部分3222n)1n(...3213222nn)1n(...321lim 31 (1)[(1) 1][2(1) 1]6limnnnnn 2111lim()326nnn 2111limlimlim326nnnnn   131lim3nSS 曲边梯形黄色部分 i-1n)(yxfini-1()nf第 i 个小曲边梯形i-1n)(yxfin第 i 个小曲边梯形阅读课本 46 页 探究，思考 i-1n)(yxfini1i( )Sfnn 第 个黄色矩形i( )nf3111( )Sfnnn 第1个黄色矩形3124( )Sfnnn 第2个黄色矩形1n1( )Sfnnn 第n个黄色矩形2 、近似代替32ni 3 、求和S黄色部分12n...SSS第 个黄色矩形第 ...