高中数学：113集合的基本运算-交集与并集 课件VIP免费

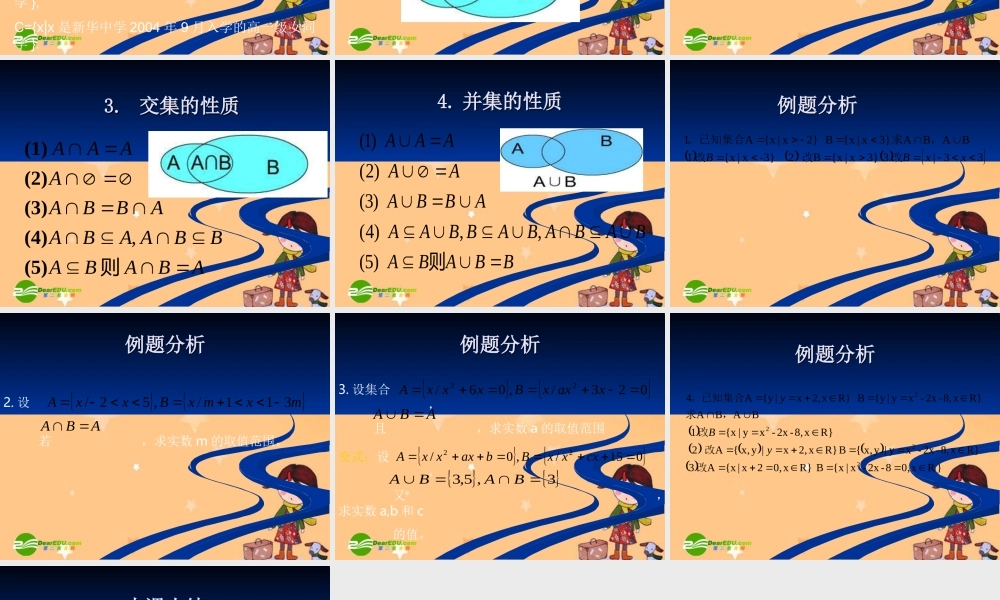
1.1.3 1.1.3 集合的基本运算集合的基本运算实数有加减乘除的基本运算，集合是否有类似的运算法则 ？ 思考思考 考察下列各个集合 , 你能说出集合 C 与集合A,B 之间的关系吗 ?(1) A={1,3,5}, B={2,4,6} ,C={1,2,3,4,5,6}(2) A={x|x 是有理数 },B={x|x 是无理数 }, C={x|x 是实数 }. 1.1. 并集并集 一般地 , 由所有属于集合 A 或属于集合 B 的元素所组成的集合 , 称为集合 A 与 B 的并集 , 记作 A∪B,( 读作“ A 并 B”). 即 A∪B={x|x∈A, 或 x∈B} 1 。 设 A={4,5,6,8}, B={3,5,7,8}, 求 A∪B.2 。 设集合 A={x|x 为等腰三角形 }, 集合 B={x|x为直角三角形 } 求 A∪B.练习练习?}7,5,3,2{}7,3{AA的所有可能的集合满足 考察下列各个集合 , 你能说出集合 A,B 与集合 C 之间的关系吗 ?(1)A={2,4,6,8,10}, B={3,5,8,12} ,C={8};(2) A={x|x 是新华中学 2004 年 9 月在校的女同学 },B={x|x 是新华中学 2004 年 9 月入学的高一级同学 },C={x|x 是新华中学 2004 年 9 月入学的高一级女同学 }.思考思考 一般地 , 由属于集合 A 且属于集合 B 的所有元素组成的集合 , 称为 A 与 B 的交集 ,记作 A∩B,( 读作“ A 交 B”), 即 A∩B={x|x∈A, 且 x∈B}.2.2. 交集交集 1 。 新华中学开运动会 , 设A={x|x 是新华中学高一年级参加百米赛跑的同学 }B={x|x 是新华中学高一年级参加跳高比赛的同学 },求 A∩B..,,,L 221的位置关系试用集合的运算表示的集合为上点直线上的点的集合为设平面内直线。2121llLll练习练习 3. 3. 交集的性质交集的性质ABABABBAABAABBAAAAA (5)(4)(3)(2) (1)则, BBABABABABABBAAABBAAAAAA则 )5(,,)4()3()2()1(4.4. 并集的性质并集的性质    33|3 3}x|{xB 2 -3}x|{x1BABA 3}x|{xB 2}x|{xA1xxBB改改改，求。已知集合例题分析例题分析 2. 设 ， 若 ，求实数 m 的取值范围。mxmxBxxA311/,52/ABA例题分析例题分析 3. 设集合 ， 且 ，求实数 a 的取值范围023/,06/22xaxxBxxxAABA变式：设 ， 又 ，求实数 a,b 和 c 的值。015/,0/22cxxxBbaxxxA 3,5,3BABA例题分析例题分析 例题分析例题分析   } Rx0,8-2x-x|{xB R}x0,2 x|{x A3 R}x8,-2x-xy|yx,{B R}x2,x|yx,{A 2 R}x8,-2x-xy|{x1 BABA R}x8,-2x-xy|{yB R}x2,x|{yA42222改改改，求。已知集合yBy 本课小结本课小结 1.1. 并集并集 2.2. 交集交集