高中数学(解析几何初步)圆的标准方程教学课件 苏教版必修2 课件VIP免费

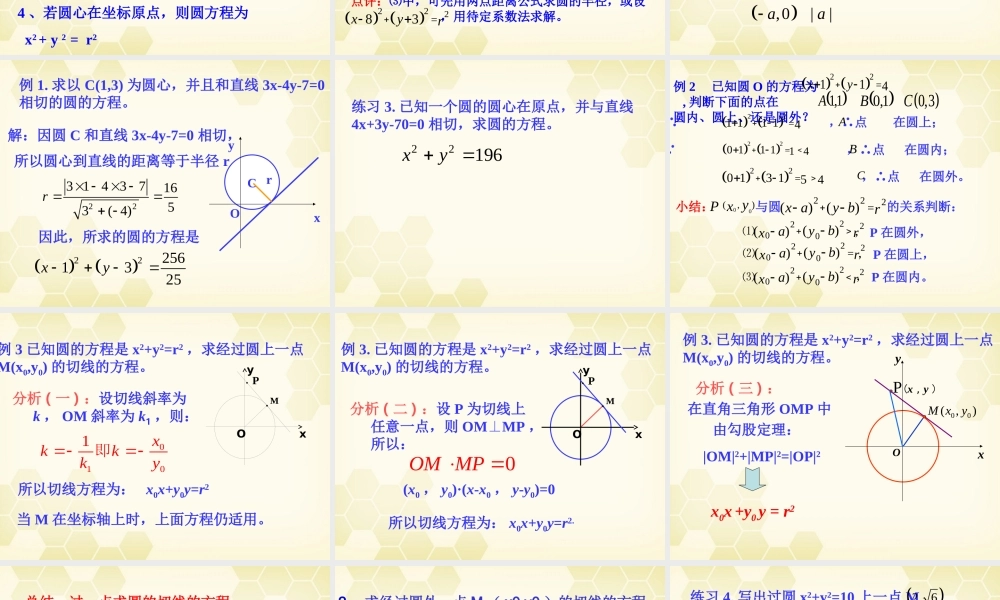
圆的标准方程问题 1 ：具有什么性质的点的轨迹称为圆？平面内与一定点距离等于定长的点的轨迹称为圆 .问题 2 ：图中哪个点是定点？哪个点是动点？动点具有什么性质？圆心和半径都反映了圆的什么特点？ 圆心 C 是定点，圆周上的点 M 是动点，它们到圆心距离等于定长 |MC|=r ，圆心和半径分别确定了圆的位置和大小．问题 3 ：求曲线的方程的一般步骤是什么？其中哪几个步骤必不可少？（ 1 ）建立适当的坐标系，用有序实数对 (x,y) 表示曲线上任意一点 M 的坐标；（ 2 ）写出适合条件 p(M) ；（ 3 ）用坐标翻译条件 p(M) ，列出方程 f(x,y)=0 ； （ 4 ）化简方程 f(x,y)=0 ； （ 5 ）证明化简后的方程为所求曲线的方程． 其中步骤 (1)(3)(4) 必不可少．用求曲线方程的一般方法来建立圆的标准方程：( , )C a br求圆心是，半径是 的圆的方程。解：设 M(x,y) 是圆上任意一点，xyO．rM据圆的定义有 |MC|=rC由距离公式，得22xaybr两边平方，得222xaybr圆的标准方程 222()()x ay br特点： 1 、是关于 x 、 y 的二元二次方程 , 无 xy 项； 2 、明确给出了圆心坐标和半径。3 、确定圆的方程必须具备三个独立条件 , 即 a 、 b 、 r .4 、若圆心在坐标原点，则圆方程为 x2 + y 2 = r2练习 1. 写出下列各圆的方程： （ 1 ）圆心在圆点，半径是 3 ；（ 3 ）经过点 P(5,1) ，圆心在点 C(8,-3)229xy22345xy（ 2 ）圆心在点 C(3,4) ，半径是 ；5228325xy点评：⑶中，可先用两点距离公式求圆的半径，或设 ，用待定系数法求解。 22283xyr练习 2. 写出下列各圆的圆心坐标和半径（ 1 ）2216xy ；（ 2 ）22129xy ；（ 3 ）222.xaya1,06（ -1 ， 2 ） 3,0||aa例 1. 求以 C(1,3) 为圆心，并且和直线 3x-4y-7=0相切的圆的方程。解：因圆 C 和直线 3x-4y-7=0 相切，所以圆心到直线的距离等于半径 r ，CxyOr223 14371653( 4)r   因此，所求的圆的方程是222561325xy练习 3. 已知一个圆的圆心在原点，并与直线4x+3y-70=0 相切，求圆的方程。22196xy例 2 已知圆 O 的方程为 , 判断下面的点在圆内、圆上、还是圆外？  22114xy...