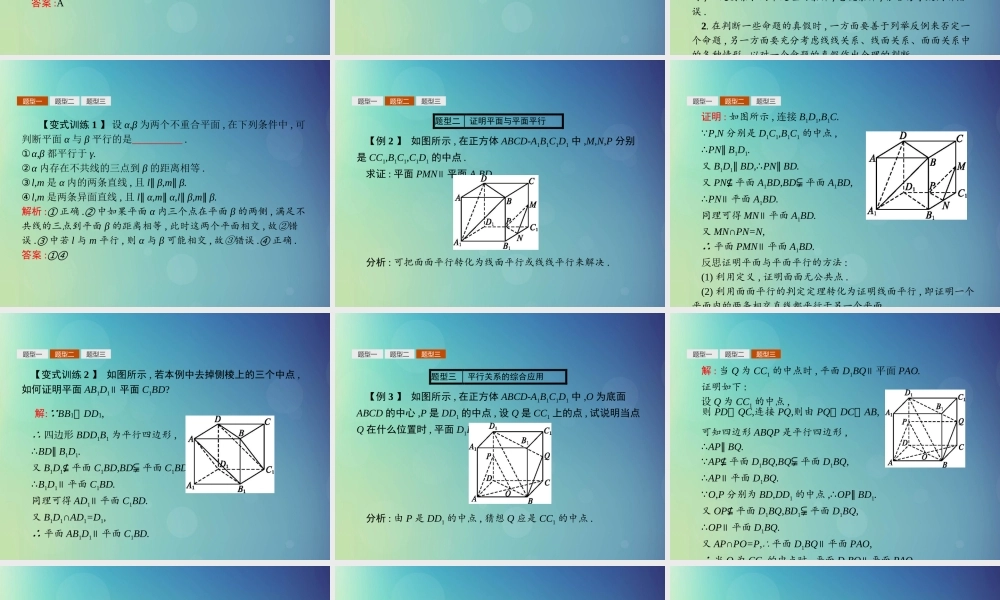
第 2 课时 平面与平面平行的判定1. 掌握面面平行的判定定理 .2. 能利用面面平行的判定定理证明面面的平行关系 .平面与平面平行的判定定理平面与平面平行的判定定理告诉我们 , 可以通过直线与平面平行来证明平面与平面平行 . 通常我们将其记为“若线面平行 , 则面面平行” .名师点拨对两个平面平行的判定定理的三点说明 :(1) 两个平面平行是指两个不重合的平面无公共点 .(2) 判断平面与平面平行问题可以转化为判断直线与平面平行问题 , 即要证明两平面平行 , 只要在其中一个平面内找到两条相交直线都与另一个平面平行 , 就可断定已知的两个平面平行 .(3) 利用判定定理证明两个平面平行时必须具备的两个条件 :①有两条直线平行于另一个平面 ;② 这两条直线必须为相交直线 .【做一做 1 】 已知直线 l,m, 平面 α,β, 且 l⫋α,m⫋α,l∥ β,m∥ β, 则 α与 β 的位置关系是 ( )A. 平行B. 相交C. 平行或相交D. 重合答案 :C【做一做 2 】 在正方体 ABCD-A'B'C'D' 中 , 与平面 ABCD 平行的平面是 ( )A. 平面 A'B'C'D'B. 平面 AA'D'DC. 平面 ABB'A'D. 平面 BCC'B'答案 :A题型一题型二题型三题型一 两平面位置关系的判断 【例 1 】 判断下列给出的各种说法是否正确 ?(1) 如果直线 a 和平面 α 不相交 , 那么 a∥ α;(2) 如果直线 a∥ 平面 α, 直线 b∥ a, 那么 b∥ α;(3) 如果直线 a∥ 平面 α, 那么经过直线 a 的平面 β∥ α;(4) 如果平面 α 内的两条相交直线 a 和 b 与平面 β 内的两条相交直线 a' 和 b' 分别平行 , 那么 α∥ β.分析 : 按照线面平行、面面平行的定义及判定定理对每个命题进行分析判断即可 .题型一题型二题型三解 :(1) 不正确 . 当直线 a 和平面 α 不相交时 , 可能有 a⫋α,a∥ α两种情况 , 当 a⫋α 时 ,a 与 α 不平行 ;(2) 不正确 . 当直线 b∥ a 时 , 如果 b⊈α, 则有 b∥ α, 如果 b⫋α, 则没有 b∥ α;(3) 不正确 . 当 a∥ α 时 , 经过直线 a 的平面 β 可能与 α 平行 , 也可能与 α 相交 ;(4) 正确 . 由线面平行的判定定理 , 知 a∥ β,b∥ β, 且 a,b⫋α,a 与 b相交 , 所以必有 α∥ β.反思 1. 运用线面平行、面面平行的判定定理判定结论是否正确时 , 一定要紧扣两个定理的条件 , 忽视条件 , ...