高中数学 211(指数与指数幂的运算2)课件 新人教A版必修1 课件VIP免费

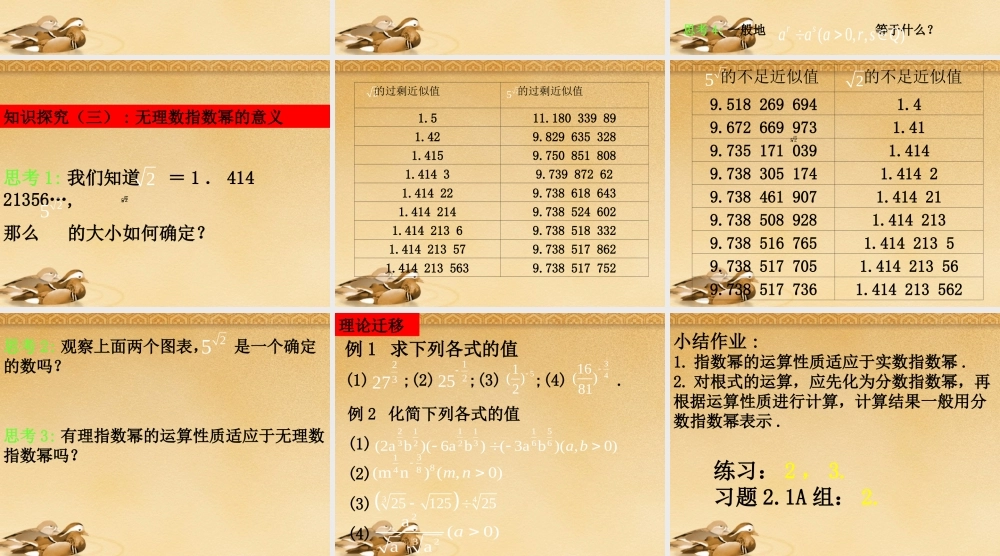
问题提出1. 什么叫 a 的 n 次方根？ 2. 设 ，则 的含义分别如何？ ,1nN n0,(0),(0)nna a aaa3. 整数指数幂有哪些运算性质？ 设 ，则 ； ； .,m nZmnm naaa()mnmnaa()nnnabab4. 有意义吗？2235 ,5知识探究（一）：分数指数幂的意义思考 2: 观察上述结论，你能总结出什么规律？思考 1: 设 a>0 ， ， ， 分别等于什么？ 510a8a124 a思考 3: 按照上述规律 , 根式 ， , 分别可写成什么形式？ 34 535757a思考 4: 我们规定： (a>0,m ， n∈N且n ＞ 1) ，那么 表示一个什么数？ 分别表示什么根式？ nnmmaa23821523 ,4思考 5: 你认为如何规定 (a>0,m,n∈N ，且 n ＞ 1) 的含义？ nma思考 6: 怎样理解零的分数指数幂的意义？ 思考 7: 都有意义吗？当 时， 何时无意义？ 233352( 2) ,( 2) ,( 2)*( ,,1)nmam nNn0a 知识探究（二） : 有理数指数幂的运算性质思考 1: = ？一般地 等于什么？ 433222(0, ,)rsaa ar sQ思考 2: = ？一般地 等于什么？ 4332(2 )() (0, ,)rsaar sQ思考 3 ： = ？一般地 等于什么？ 223323(0, ,)rsaa ar sQ思考 4: 一般地 等于什么？ (0, ,)rsaa ar sQ知识探究（三） : 无理数指数幂的意义思考 1: 我们知道 ＝ 1 ． 414 21356…,那么 的大小如何确定？252225 225 的过剩近似值 的过剩近似值1.511.180 339 891.429.829 635 3281.4159.750 851 8081.414 39.739 872 621.414 229.738 618 6431.414 2149.738 524 6021.414 213 69.738 518 3321.414 213 579.738 517 8621.414 213 5639.738 517 75222525225 2 的不足近似值 的不足近似值9.518 269 6941.49.672 669 9731.419.735 171 0391.4149.738 305 1741.414 29.738 461 9071.414 219.738 508 9281.414 2139.738 516 7651.414 213 59.738 517 7051.414 213 569.738 517 7361.414 213 562思考 3: 有理指数幂的运算性质适应于无理数指数幂吗？ 思考 2: 观察上面两个图表， 是一个确定的数吗？ 25例 1 求下列各式的值 (1) ;(2) ;(3) ;(4) . 2327122551( )23416()81理论迁移例 2 化简下列各式的值(1)(2)(3)(4)211511336622(2a b )( 6a b )( 3a b )( ,0)a b 31884(m n) ( ,0)m n342512525232a(0)aaa 小结作业 :1. 指数幂的运算性质适应于实数指数幂 .2. 对根式的运算，应先化为分数指数幂，再根据运算性质进行计算，计算结果一般用分数指数幂表示 .练习： 2 ， 3.习题 2.1A 组： 2.