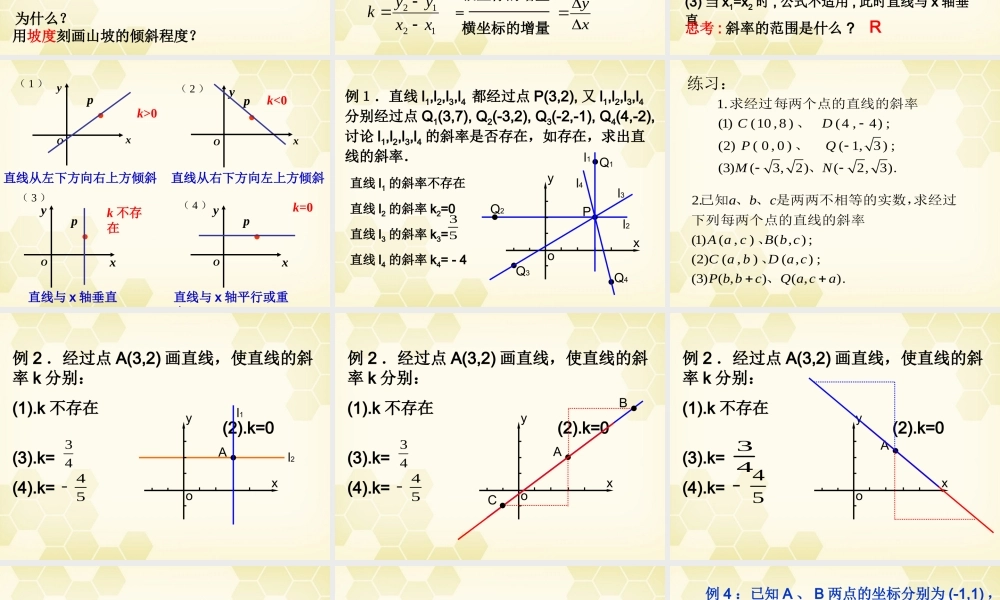
引言 : 通过坐标系把点和坐标、曲线和方程联系起来,使形和数结合,是研究几何图形的一种重要的方法。 在本章中,我们将学习用代数方法研究几何问题的初步知识。 我们将学习直线和圆的方程、这些知识是进一步学习圆锥曲线方程的基础。 ( 一 ) 复习一次函数及其图象 已知一次函数 y=2x+1 ,试判断点 A(1 ,3) 和点 B(2 , 1) 是否在函数图象上.初中我们是这样回答的: A(1,3) 的坐标满足函数式,∴ 点 A 在函数图象上. B(2 , 1) 的坐标不满足函数式,∴ 点 B 不在函数图象上. 1. 在同一坐标系中作出下列函数的图像:⑴y=x+1 ; ⑵ y=2x+1 ; ⑶ y=-x+1.xyo(0 ,1)2. 三个图象有什么相同和不同的地方 ?相同点 : 都过 (0,1)不同点 : 倾斜程度不同 上图为环法自行车赛某日路线图的一部分OA 、 AB 两段哪段路程消耗运动员体力更多?为什么?用坡度刻画山坡的倾斜程度?OABCDE900m900m800mB1300mA1高度坡度宽度 P(x1, y1)Q(x2, y2)Oxy2.1.1 直线的斜率1212xxyyk直线 PQ 的斜率纵坐标的增量横坐标的增量xy 斜率公式)( :),(),,(211212222111xxxxyykyxPyxP的直线的斜率公式经过两点公式的特点 :(1) 与两点的顺序无关 ;(2) 公式表明 , 直线对于 x 轴的倾斜度 , 可以通过直线上任意两点的坐标来表示(3) 当 x1=x2 时 , 公式不适用 , 此时直线与 x 轴垂直思考 : 斜率的范围是什么 ?R x.pyO( 3 )k 不存在x.pyO( 2 )k<0x.pyO( 1 )k>0.y( 4 )xpOk=0直线从左下方向右上方倾斜直线从右下方向左上方倾斜直线与 x 轴平行或重合直线与 x 轴垂直 例1.直线 l1,l2,l3,l4 都经过点 P(3,2), 又 l1,l2,l3,l4分别经过点 Q1(3,7), Q2(-3,2), Q3(-2,-1), Q4(4,-2), 讨论 l1,l2,l3,l4 的斜率是否存在,如存在,求出直线的斜率.直线 l1 的斜率不存在直线 l2 的斜率 k2=0直线 l3 的斜率 k3=直线 l4 的斜率 k4= - 453l2l3l4l1Q4Q3Q2Q1Pxoy 1.(1)(10 ,8 )(4 ,4) ;(2)( 0 , 0 )( 1, 3) ;(3)(3,2)(2,3).CDPQMN求经过每两个点的直线的斜率、、、2.(1)( ,)( , ) ;(2)( ,)( , ) ;(3) ( ,)( ,).abcA a cB b cC a bD a cP b bcQ a ca已知 、 、 是两两不相等的实数,求经过下列每两个点的直线的斜率、、、练习: 例 2 .经过点 A(3,2) 画直线,使直线的斜率 k 分...