高考数学 8.2 空间几何体的表面积与体积总复习课件VIP免费

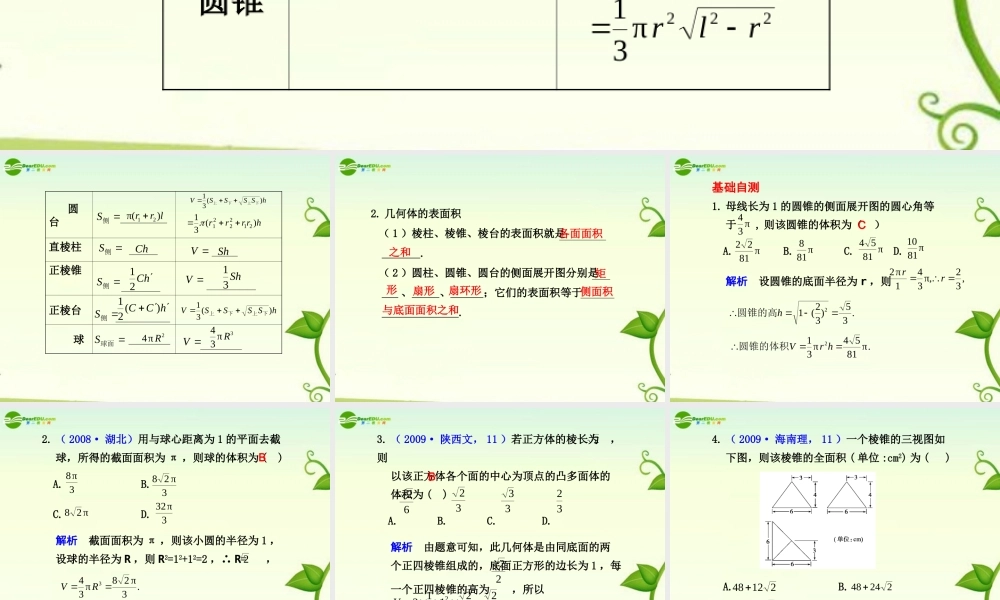
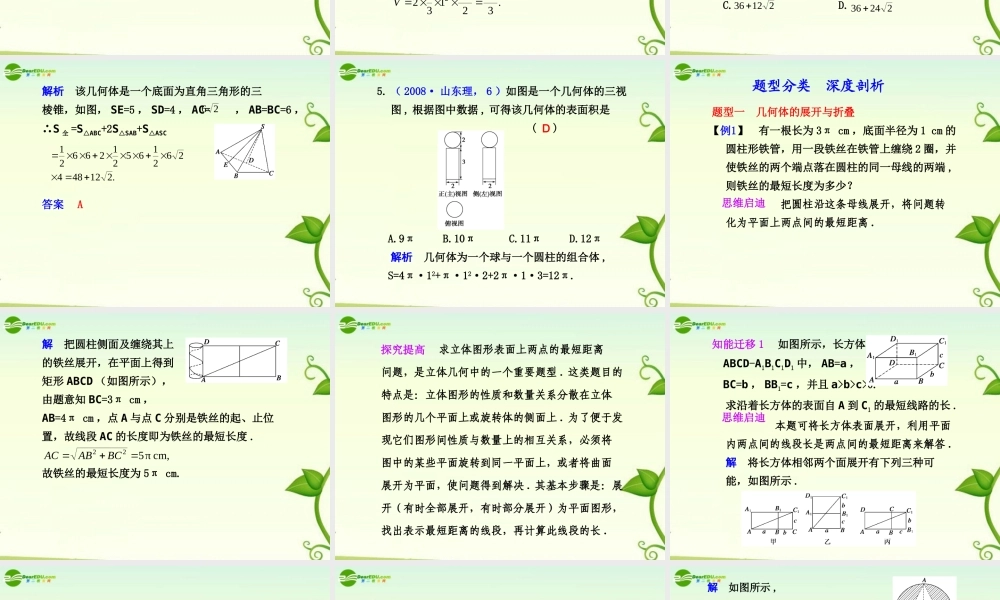
§8.2 空间几何体的表面积与体积要点梳理1. 柱、锥、台和球的侧面积和体积： 面积 体积圆柱 圆锥侧Srhπ2VShhr2π侧SrlπVhr2π31222π31rlr基础知识 自主学习Sh31 圆台直棱柱正棱锥正棱台 球侧Slrr)π(21 hSSSSV)(31下上下上hrrrr)(31212221 侧SChVSh侧ShC 21VSh31侧ShCC)(21hSSSSV)(31下上下上球面S2π4 RV3π34R2. 几何体的表面积 （ 1 ）棱柱、棱锥、棱台的表面积就是 . （ 2 ）圆柱、圆锥、圆台的侧面展开图分别是 、 、 ；它们的表面积等于 .各面面积之和矩形扇形扇环形侧面积与底面面积之和基础自测1. 母线长为 1 的圆锥的侧面展开图的圆心角等 于 , 则该圆锥的体积为（ ） A. B. C. D. 解析 设圆锥的底面半径为 r ，则π34π8122π818π8154π8110,32π,341π2rr.35)32(12 h圆锥的高.π8154π312 hrV圆锥的体积C2. （ 2008· 湖北）用与球心距离为 1 的平面去截 球，所得的截面面积为 π ，则球的体积为 ( ) A. B. C. D. 解析 截面面积为 π ，则该小圆的半径为 1 ， 设球的半径为 R ，则 R2=12+12=2 ，∴ R= ，3π83π28π283π322.3π28π343 RVB3. （ 2009· 陕西文， 11 ）若正方体的棱长为 ，则 以该正方体各个面的中心为顶点的凸多面体的 体积为 ( ) A. B. C. D. 解析 由题意可知，此几何体是由同底面的两 个正四棱锥组成的，底面正方形的边长为 1 ，每 一个正四棱锥的高为 ，所以6232333222.322213122VB24. （ 2009· 海南理， 11 ）一个棱锥的三视图如 下图，则该棱锥的全面积 ( 单位 :cm2) 为 ( ) A. B. C. D.2124821236 22436 22448解析 该几何体是一个底面为直角三角形的三棱锥，如图， SE=5 ， SD=4 ， AC= ， AB=BC=6 ，∴S 全 =S△ABC+2S△SAB+S△ASC答案 A.2124842621652126621265. （ 2008· 山东理， 6 ）如图是一个几何体的三视 图 , 根据图中数据 , 可得该几何体的表面积是 ( ) A.9π B.10π C.11π D.12π 解析 几何体为一个球与一个圆柱的组合体 , S=4π·12+π·12·2+2π·1·3=12π.D题型一 几何体的展开与折叠 有一根长为 3π cm ，底面半径为 1 cm 的 圆柱形铁管，用一段铁丝在铁管上缠绕 2 圈，并 使铁丝的两...