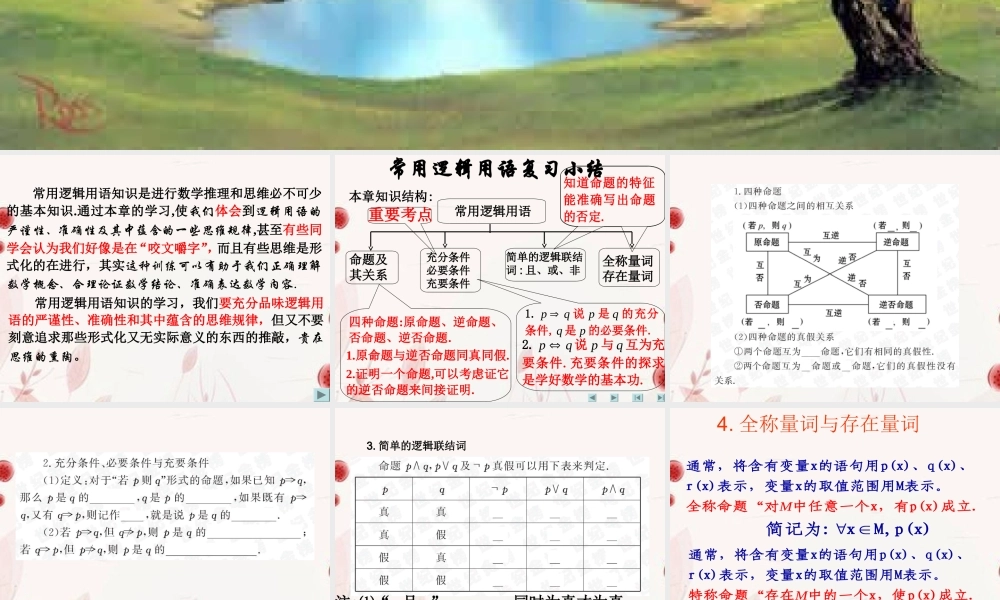
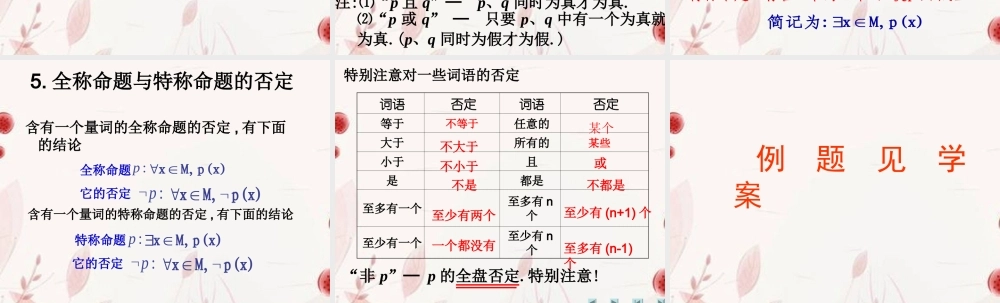
常 用 逻 辑 用 语 复 习 常用逻辑用语知识是进行数学推理和思维必不可少的基本知识.通过本章的学习,使我们体会到逻辑用语的严谨性、准确性及其中蕴含的一些思维规律,甚至有些同学会认为我们好像是在“咬文嚼字”,而且有些思维是形式化的在进行,其实这种训练可以有助于我们正确理解数学概念、合理论证数学结论、准确表达数学内容. 常用逻辑用语知识的学习,我们要充分品味逻辑用语的严谨性、准确性和其中蕴含的思维规律,但又不要刻意追求那些形式化又无实际意义的东西的推敲,贵在思维的熏陶。 常用逻辑用语复习小结 本章知识结构: 常用逻辑用语命题及其关系全称量词存在量词充分条件必要条件充要条件简单的逻辑联结词 : 且、或、非四种命题:原命题、逆命题、否命题、逆否命题. 1.原命题与逆否命题同真同假. 2.证明一个命题,可以考虑证它的逆否命题来间接证明. 1. pq说 p 是 q 的充分条件, q 是 p 的必要条件. 2. pq说 p 与 q 互为充要条件.充要条件的探求是学好数学的基本功. 知道命题的特征.能准确写出命题的否定. 重要考点 注:⑴“p 且 q”─ p、q 同时为真才为真. ⑵“p 或 q” ─ 只要 p、q 中有一个为真就为真.(p、q 同时为假才为假.) 3. 简单的逻辑联结词4. 全称量词与存在量词M通常,将含有变量x的语句用p(x)、q(x)、r(x)表示,变量x的全称命题“对中任意一个x,取值范围有p(x用M表示。)成立. 简记为: xM,p(x)M通常,将含有变量x的语句用p(x)、q(x)、r(x)表示,变量x特称命题“存在中的一个x的取值范围用,使p(xM表示。)成立. 简记为: xM,p(x)5. 全称命题与特称命题的否定含有一个量词的全称命题的否定 , 有下面的结论 xM,p(x)全称命题 :p含有一个量词的特称命题的否定 , 有下面的结论 xM,p(x)特称命题:p它的否定:p xM, p(x)它的否定:p xM, p(x)特别注意对一些词语的否定词语否定词语否定等于任意的大于所有的小于且是都是至多有一个至多有 n个至少有一个至少有 n个“非 p”─ p 的全盘否定.特别注意! 不等于某个不大于某些不小于或不是不都是至少有两个一个都没有至少有 (n+1) 个至多有 (n-1)个 例 题 见 学 案