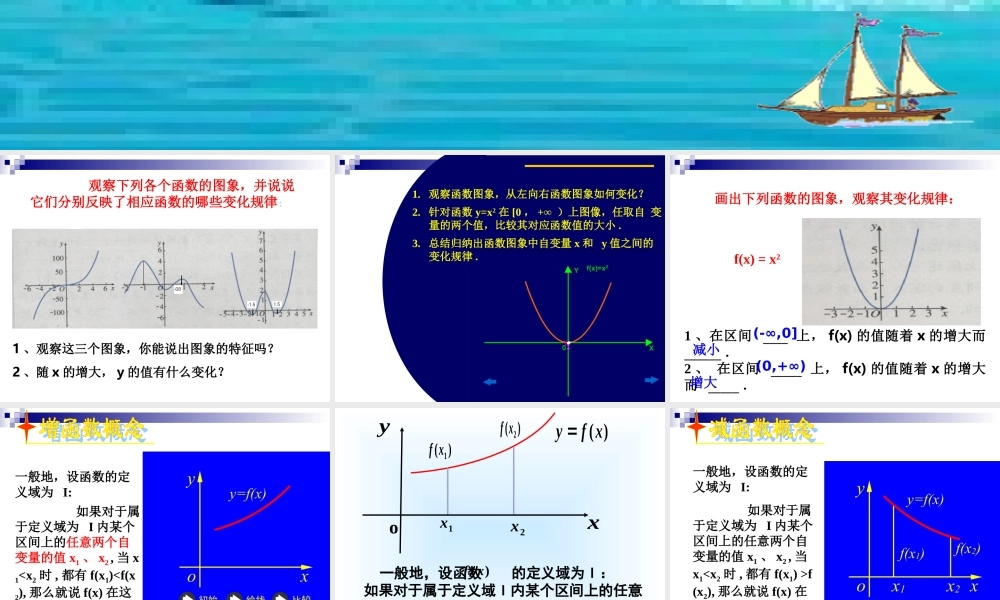
观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律: 1 、观察这三个图象,你能说出图象的特征吗?2 、随 x 的增大, y 的值有什么变化? 1. 观察函数图象,从左向右函数图象如何变化?2. 针对函数 y=x2 在 [0 , +∞ )上图像,任取自 变量的两个值,比较其对应函数值的大小 .3. 总结归纳出函数图象中自变量 x 和 y 值之间的变化规律 . 1 、在区间 ____ 上, f(x) 的值随着 x 的增大而 ______ .2 、 在区间 _____ 上, f(x) 的值随着 x 的增大而 _____ . f(x) = x2(-∞,0](0,+∞)增大减小画出下列函数的图象,观察其变化规律: 一般地,设函数的定义域为 I: 如果对于属于定义域为 I 内某个区间上的任意两个自变量的值 x1 、 x2 , 当 x1f(x2), 那么就说 f(x) 在这个区间上是减函数 .1x2x)(1xf)(2xfxyo 一般地,设函数 的定义域为 I : 如果对于属于定义域 I 内某个区间上的任意两个自变量的值 , 。当 时,都有 那么就说 在这个区间上是减函数。)(xf1x2x21xx )()(21xfxf)(xf 如果函数 在某个区间上是增函数或减函数,那么就说函数 在这一区间具有(严格的)单调性,)(xfy )(xfy 这一区间叫做 的单调区间。)(xfy 1. 函数的单调性也叫函数的增减性2. 函数的单调性是对某个区间而言 的 , 它是一个局部概念 .注: 例 1 下图是定义在闭区间 [-5,5] 上的函数 的图象 , 根据图象说出的单调区间 , 以及在每一区间上 ,是增函数还是减函数 .)(xfy )(xfy )(xfy -212345-23-3-4-5-1-112xyO -212345-23-3-4-5-1-112xy在区间 [-5,-2), [1,3) 上是减函数在区间 [-2,1), [3,5) 上是增函数 .解 : 函数 的单调区间有[-5,-2), [-2,1), [1,3), [3,5],)(xfy O 12-2-1-11xyo如图 , 已知 的图象 ( 包括端点 ),根据图象说出函数的单调区间 , 以及在每一区间上 ...