高一数学 对数三 ppt 教案VIP免费

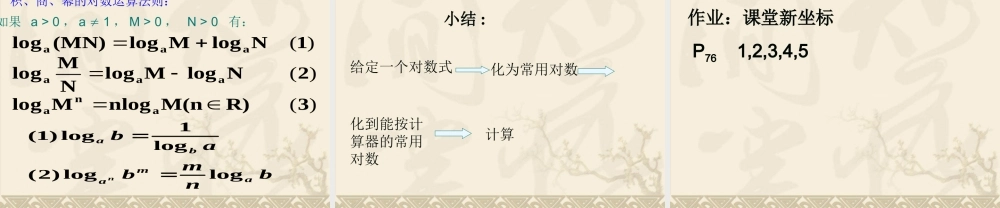
知识复习1 、对数的运算性质R)M(nnlogM(3)logNlog-MlogNM(2)logN;logMlog(MN)log10,0NM1,a0,aanaaaaaaa）（那么如果malogna2manloga式、两个常用的对数恒等 的值呢？ 出值来，那么如何计算等一些特殊的对数能求诸如新课引入：2log27log,21log1.0832 我们可以通过计算器求出 lgN 与lnN ，但对于不同底的对数函数如何求，我们今天就来解决这个问题。 208.1x2lg08.1lgx两边取常用对数得2lg08.1lgx即08.1lg2lgx所以90334.03010.0x按计算器得至此我们已完整的解决了我们的问题，那么我们能否得出一般性的结论呢？ 比如 x=logaN,到底等于多少？是否有一般性结论 abbccalogloglog:1求证例bnmbabamabanloglog)2(log1log)1( 这就是著名的换底公式，通过这个公式我们可以把任何对数化成我们所需要的底，然后通过按计算器。他有以下两个推论，请同学们证明5lg12lg12log5x例如 aNNccalogloglog)0),,1()1,0(,(Nca证明：设 由对数的定义可以得： ,paN 即证得 pNalog,loglogpccaN ,loglogapNccaNpccloglogaNNccalogloglog这个公式叫做换底公式换底公式 推论 ( 一 )abbalog1log),1()1,0(,ba证明 : 由换底公式 取以 b 为底的对数得： 还可以变形 , 得 ,1logbbaNNccalogloglogabbbbalogloglogabbalog1log1loglogabba NmnNanamloglog证明：设 ,logpN nam由对数的定义可以得： ,)(pmnaN ∴即证得 NmnNanamloglogmpnaN pnmNa logpnmaN 推论 ( 二 ) 讲解范例 例二 8log7log3log732解 :8log7log3log7322lg3lg2lg2lg32lg2lg3=33lg7lg7lg8lg 235111(2):logloglog2589计算252552432(3):log32(log 3log 9log3 )求值例三 ：（ 1 ）已知 log427=a ， log52=b ，求lg2 ， lg3 。.,0111,,1,,.5的值求且的正数是不等于设abczyxcbacbazyx3lg32(1)abblg 21bb 122521 2lglg2lg(2 )log.xxyxyy2.已知求的值22lg()lg(2 )(2 )xyxyxyxy由已知得22540.xxyy20,20.xyxy  2224loglog4log ( 2)4xy解：( - )( -4 )0.4x yxyxyxy 即或().4xyxy 舍去 即 提高练习：33333lg 2.lg5(2)lg5,lg 2?lg 20?(3)2,83611(4)lg(1),lg(1).981(1)(lg2)(lg5)loglog3naab...