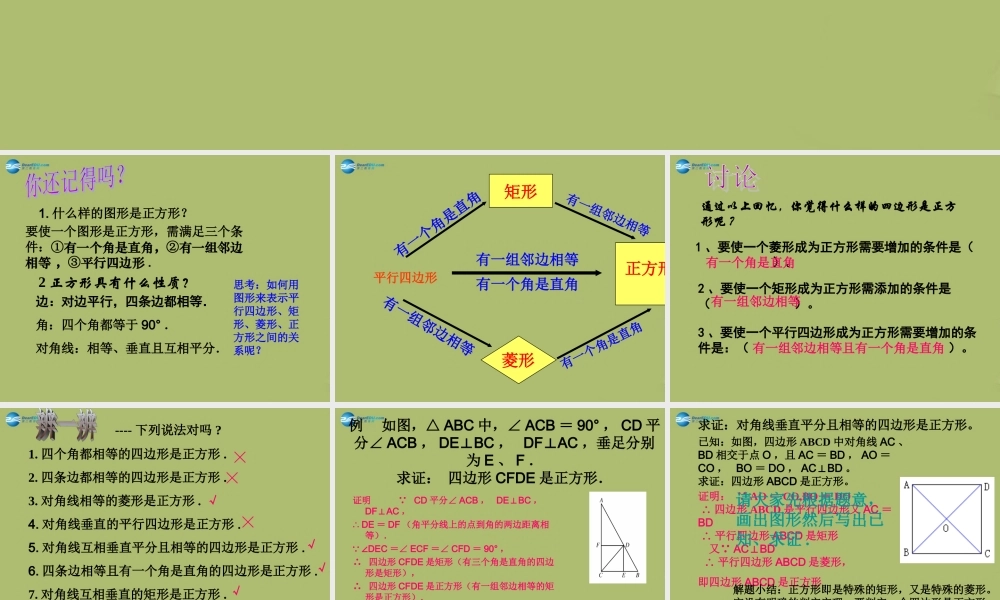
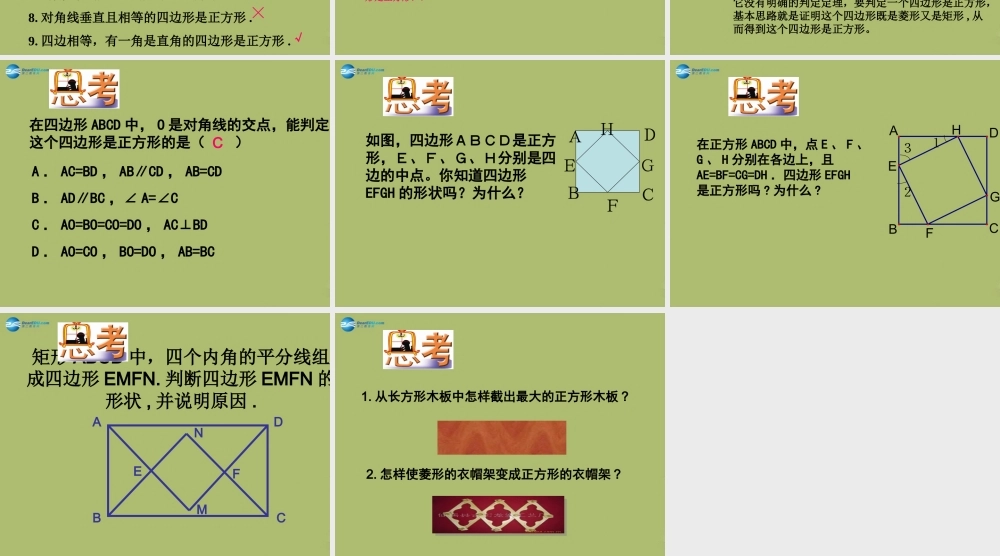
正方形的判定第 19 章 矩形、菱形与正方形19.3 正方形(第 2 课时)要使一个图形是正方形,需满足三个条件:①有一个角是直角,②有一组邻边相等 ,③平行四边形 .1. 什么样的图形是正方形?2 正方形具有什么性质?边:对边平行,四条边都相等.角:四个角都等于 90° .对角线:相等、垂直且互相平分.思考:如何用图形来表示平行四边形、矩形、菱形、正方形之间的关系呢?正方形矩形有一组邻边相等菱形有一个角是直角有一组邻边相等有一个角是直角平行四边形有一个角是直角有一组邻边相等通过以上回忆,你觉得什么样的四边形是正方形呢 ?1 、要使一个菱形成为正方形需要增加的条件是( )。2 、要使一个矩形成为正方形需添加的条件是( )。3 、要使一个平行四边形成为正方形需要增加的条件是:( )。有一个角是直角有一组邻边相等有一组邻边相等且有一个角是直角 ---- 下列说法对吗 ?1. 四个角都相等的四边形是正方形 . 2. 四条边都相等的四边形是正方形 .3. 对角线相等的菱形是正方形 .4. 对角线垂直的平行四边形是正方形 .5. 对角线互相垂直平分且相等的四边形是正方形 .6. 四条边相等且有一个角是直角的四边形是正方形 .7. 对角线互相垂直的矩形是正方形 .8. 对角线垂直且相等的四边形是正方形 .9. 四边相等,有一角是直角的四边形是正方形 .╳√╳╳√√√╳√例如图,△ ABC 中,∠ ACB = 90° , CD 平分∠ ACB , DEBC⊥, DFAC⊥,垂足分别为 E 、 F .求证: 四边形 CFDE 是正方形.证明 CD 平分∠ ACB , DEBC⊥, DFAC⊥, ∴ DE = DF (角平分线上的点到角的两边距离相等). ∠DEC =∠ ECF =∠ CFD = 90° ,∴ 四边形 CFDE 是矩形(有三个角是直角的四边形是矩形),∴ 四边形 CFDE 是正方形(有一组邻边相等的矩形是正方形).求证:对角线垂直平分且相等的四边形是正方形。 已知:如图,四边形 ABCD 中对角线 AC 、BD 相交于点 O ,且 AC = BD , AO =CO , BO = DO , ACBD⊥。求证:四边形 ABCD 是正方形。证明: AO = CO,BO = DO ∴ 四边形 ABCD 是平行四边形又 AC =BD ∴ 平行四边形 ABCD 是矩形 又 ACBD⊥ ∴ 平行四边形 ABCD 是菱形,即四边形 ABCD 是正方形解题小结:正方形即是特殊的矩形,又是特殊的菱形。它没有明确的判定定理,要判定一个四边形是正...