八年级数学上册 14.2.2 完全平方公式课件 (新版)新人教版 课件VIP免费

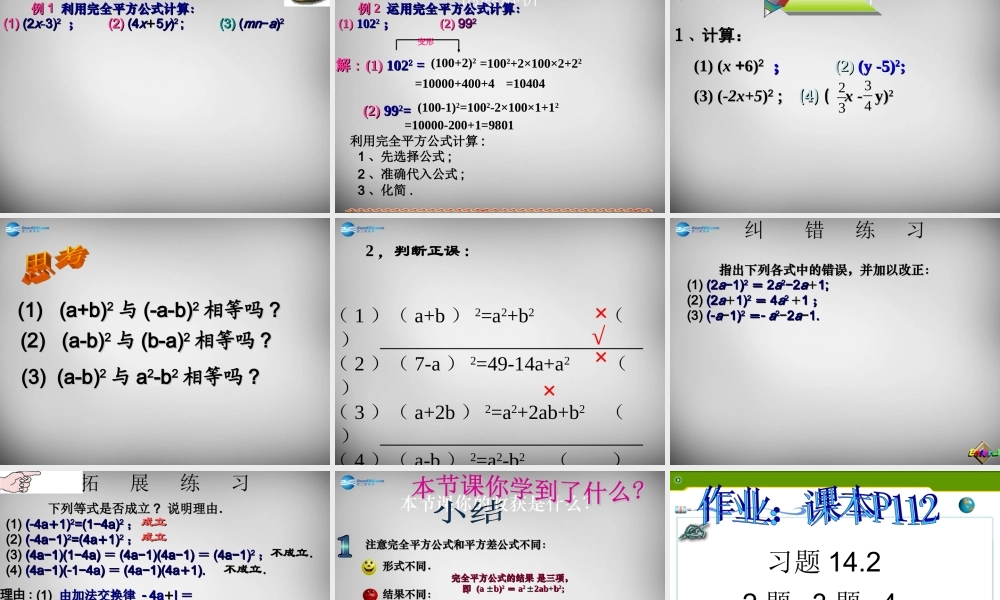
14.2.2 乘法公式回顾与思考aa2 2 −− bb22;; 平方差公式平方差公式平方差公式平方差公式应用平方差公式的注意事应用平方差公式的注意事项项 :: 回顾 回顾 && 思思考考☞☞((aa++bb)()(aa−−bb))==☾☾ 弄清在什么情况下才能使用平方差公式弄清在什么情况下才能使用平方差公式 ::12)12)(12)(12 xxx1)1)(1)(22 xxx2224)2)(4baba222))(5baba222))(6baba√加油啊！2)ba （baba22bababa222baba2)-ba（baba--22--bababa22 2-baba结论 1:222()2abaabb结论 2:222()2abaabbbbaa2)(ba(a+b)²a²2ab²2bababab2++完全平方和公式：完全平方公式 的图形理解aa-bba-bab2222)(bababa两数和的平方，等于它们的平两数和的平方，等于它们的平方和加上它们的积的两倍。方和加上它们的积的两倍。2222)(bababa2222)(bababa两数和的平方，等于它们的平两数和的平方，等于它们的平方和加上它们的积的两倍。方和加上它们的积的两倍。两数差的平方，等于它们的平两数差的平方，等于它们的平方和，减去它们的积的两倍。方和，减去它们的积的两倍。加油思考！2222)(bababa2222)(bababa集思广益哦！公式特点：4 、公式中的字母 a ， b 可以表示数，单项式和 多项式。(a+b)(a+b)22= a= a22 +2ab+b +2ab+b22(a(a--b)b)22= a= a22 -- 2ab+b 2ab+b221 、积为二次三项式；2 、积中两项为两数的平方和；3 、另一项是两数积的 2 倍，且与乘式中 间的符号相同。 首平方，尾平方，积的 2 倍在中央 例题解析学一学学一学  例例 1 1 利用完全平方公式计算：利用完全平方公式计算：(1)(1) (2(2xx−−3)3)22 ； ； (2)(2) (4(4xx++55yy))2 2 ; ; (3)(3) ( (mnmn−−aa))22 例题解析 学一学学一学  例例 22 运用完全平方公式计算：运用完全平方公式计算：(1)(1) 102 10222 ； ； (2)(2) 999922解解 :: (1)(1) 102 1022 2 == (100+2)2变形(2)(2) 99 9922===1002+2×100×2+22=10000+400+4=10404(100-1)2=1002-2×100×1+12=10000-200+1=98012 、准确代入公式 ;利用完全平方公式计算 :1 、先选择公式 ;3 、化简 .随堂练习随堂练习随堂练习 (1) (1) ((x x ++66))22 ； ； (2)(2) (y -5) (y -5)22; ; (3) (3) ((-2x+...