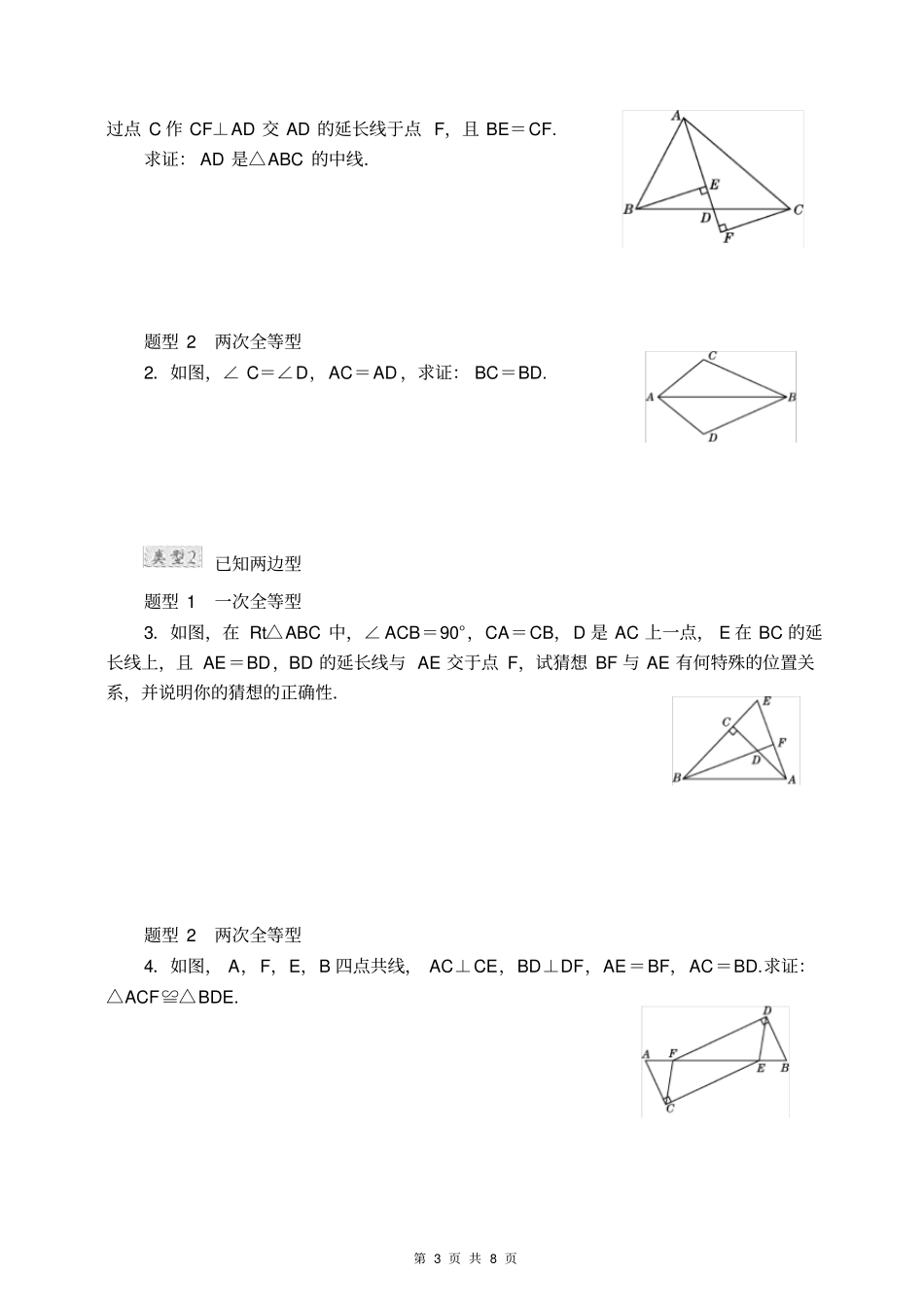
第 1 页 共 8 页华师大版八年级上册数学《全等三角形》重难点专训专训一:命题与定理名师点金: 命题贯穿于数学始终, 是数学的基础知识, 学习时, 要会判断一句话是不是命题,能找出命题的条件和结论, 会判断命题的真假, 会用证明的方法去证明一个真命题.命题的定义及结构1.下列句子是命题的有 ()①一个角的补角比这个角的余角大多少度?②垂线段最短,对吗?③等角的补角相等;④两条直线相交只有一个交点;⑤同旁内角互补.A.1 个B.2 个C.3 个D.4 个2.写出下列命题的条件和结论.(1)平行于同一条直线的两直线平行;(2)互为邻补角的两个角的平分线互相垂直;(3)两点确定一条直线.命题的真假3.判断下列命题是真命题还是假命题,若是假命题,请说明理由.(1)一个三角形如果有两个角互余,那么这个三角形是直角三角形;(2)如果 a 是有理数,那么a2+1>0;(3)如果 AC=BC,那么点 C 是 AB 的中点;(4)如果等腰三角形的两条边长分别为5 和 7,那么这个等腰三角形的周长为17.第 2 页 共 8 页命题的证明类型 1 证明真命题4.如图所示, AB∥CD,直线 EF 与 AB ,CD 分别交于点 M,N,∠ BMN 与∠ DNM的平分线相交于点G.求证: MG⊥NG.请补全下面的证明过程:证明: MG 平分∠ BMN(____________),∴∠GMN =12∠BMN(____________________).同理∠ GNM =12∠DNM. AB ∥CD(____________),∴∠BMN +∠ DNM =________(____________),∴∠GMN +∠ GNM =________(____________), ∠GMN +∠ GNM +∠ G=________(________),∴∠G=________,∴MG⊥NG(____________).类型 2 证明假命题5.已知命题:“一个锐角与一个钝角的度数之和一定等于180°”,请你判断这个命题的真假,如果是假命题,请你用举反例的方法说明它是假命题.专训二:全等三角形判定的三种类型名师点金: 一般三角形全等的判定方法有四种:S.S.S.,S.A.S.,A.S.A.,A.A.S.;直角三角形是一种特殊的三角形, 它的判定方法除了上述四种之外,还有一种特殊的方法, 即“H.L. ”.具体到某一道题目时,要根据题目所给出的条件进行观察、分析,选择合适的、简单易行的方法来解题.已知一边一角型题型 1 一次全等型1.如图,在△ ABC 中, D 是 BC 边上一点,连接AD,过点 B 作 BE⊥AD 于点 E,第 3 页 共 8 页过点 C 作 CF⊥AD 交 AD 的延长线于点 F,且 BE=CF.求证:...