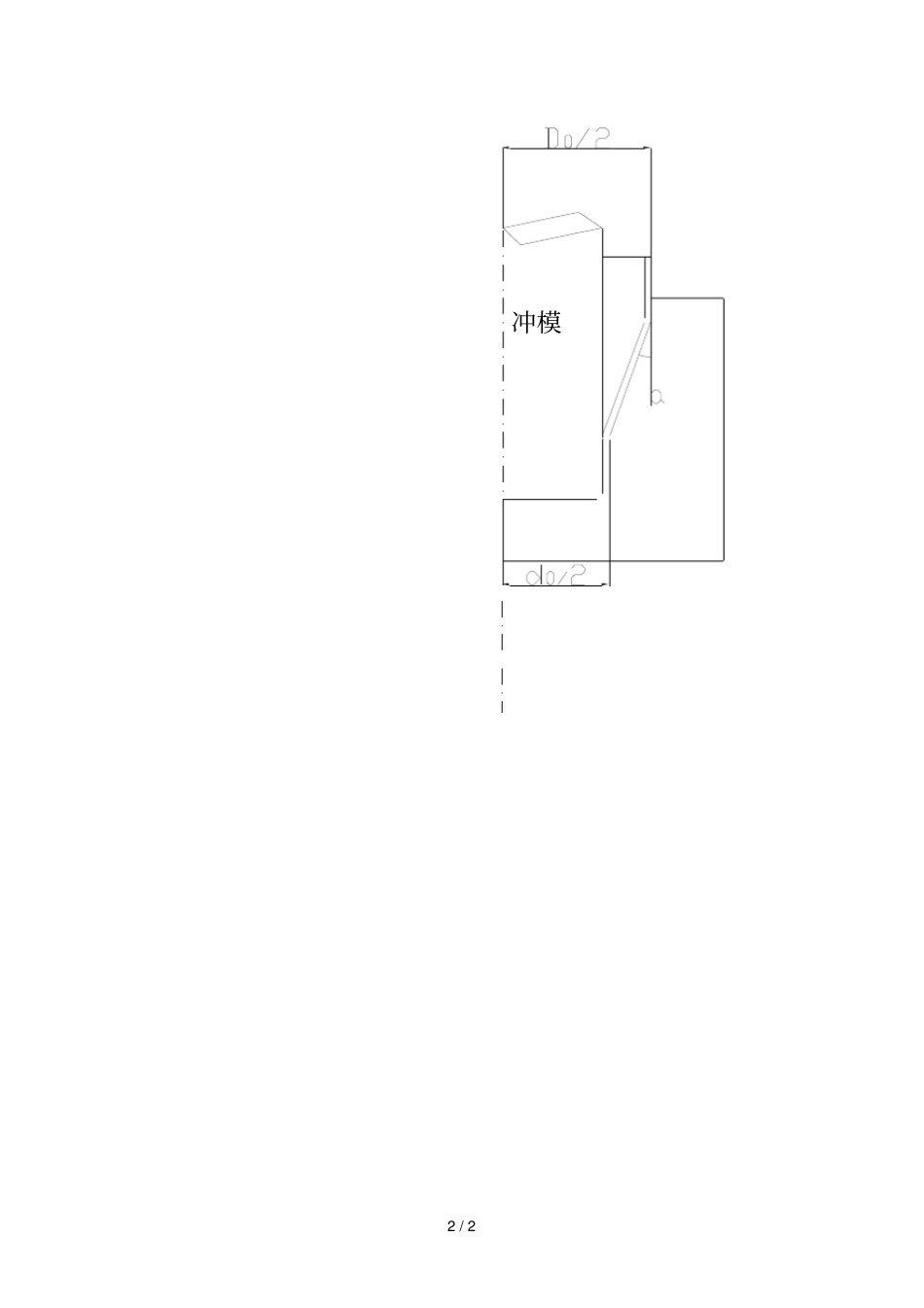
1 / 2 第三部分塑性力学1、设有一高为H 的长方体均匀变形,已知顶端质点的小量级的压下量为0u ,底面的质点静止不动,将中心线取作Oz 轴, O 为底面的形心,Ox 轴与 Oy 轴分别平行于长方体的两条水平横线,试由体积不变这一条件出发,证明该长方体的位移场为000,,22xyzxyzuuuuuuHHH2、设有一高为H 的圆柱体,先均匀拉伸到2H,再均匀压缩回H,设在变形过程中体积保持不变,试分别求出这两个阶段的对数应变、等效对数应变及最终的对数应变、等效对数应变?3、设薄球壳的半径为R,厚度为t( tR ),承受内压P,试用 Mises 屈服准则求薄球壳屈服时的内压P?4、有一刚塑性硬化材料,其硬化曲线、也即等效应力-应变曲线为200(1)MPa 。质点承受两向压力,应力主轴始终不变。试按下列两种加载路线分别求出最终的塑性全量主应变123,,:a)主应力从 0 开始直接按比例加载到最终主应力状态为(300,0,-200)MPa。b)主应力从 0 开始按比例加载到(150,0,100)MPa,然后按比例变载到(300,0,-200)MPa。5、已知刚塑性变形体中的某质点处的平面应力张量为6030030030MPa,应变分量xd(0 为一微量),试求应变增量张量及塑性功增量密度。6、设有薄壁圆筒,半径为r,两端面是半径为r 的薄壁半球壳,设壁厚全部为t,承受内压 p。设圆筒为Mises 刚塑性材料,屈服应力为s 。试求:(1)不计径向应力r ,确定圆筒与半球壳哪一部分先屈服?(2)设屈服时的等效应变增量为0 ,试求对应的应变增量张量?7、设圆柱体在平行砧板之间镦粗,高度为H,半径为 R0,真实应力为,摩擦应力为,试用主应力法求镦粗时的的单位流动压力。8、大圆柱拉深为小圆筒,如图示,设变形只发生在工件的圆锥面上,锥面与轴线的夹角为,不计接触面上的摩擦应力,且忽略凹模出口处的弯曲效应,圆筒的 t 且在拉深时保持不变,试用主应力法求拉深力?2 / 2 冲模