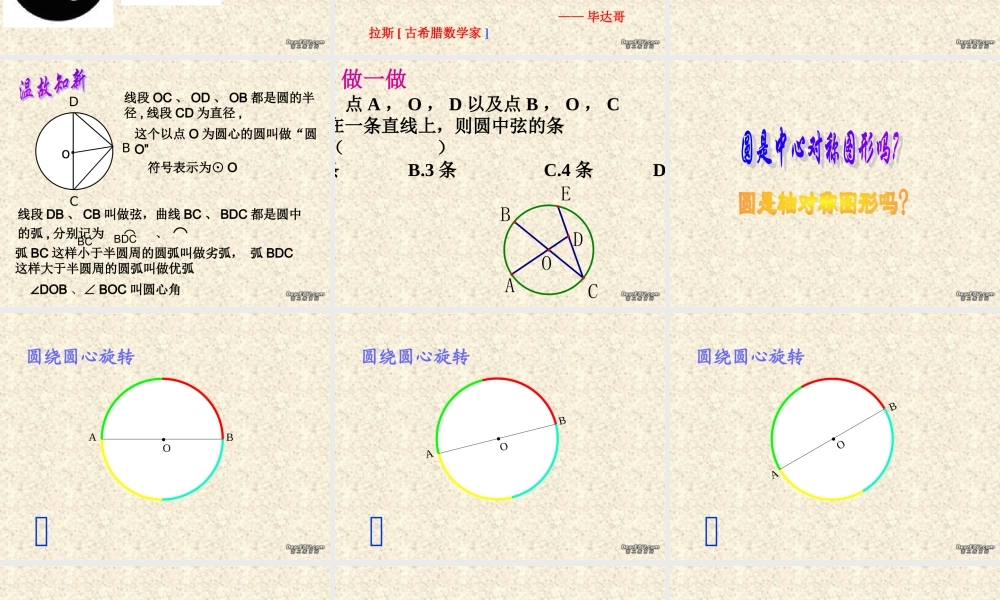
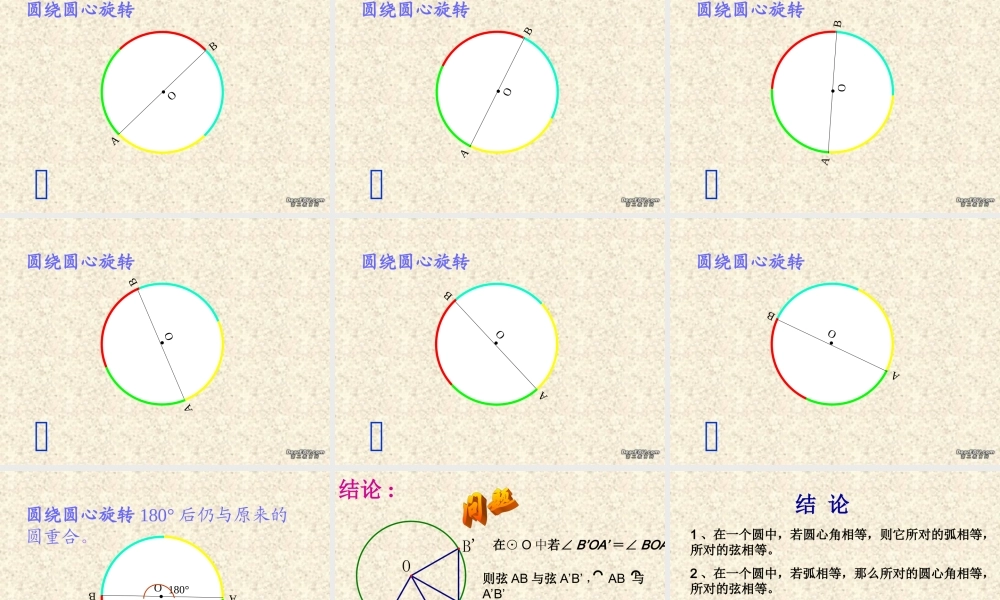
圆的认识( 1 )日月贝民族乐器—— 月琴民族乐器——阮精美的月亮门福建客家土楼天坛祈年殿古罗马斗兽场城市立体交通天安门广场国庆花坛平面设计图案中的“圆”一切平面图形中,最美的是圆! —— 毕达哥拉斯 [ 古希腊数学家 ].AO即:在平面内 , 圆是到定点的距离等于定长的点的集合 . 定义:平面上到定点的距离等于图形叫圆 .定长的所有点组成的BDCo线段 OC 、 OD 、 OB 都是圆的半径 , 线段 CD 为直径 ,这个以点 O 为圆心的圆叫做“圆O”符号表示为⊙ O线段 DB 、 CB 叫做弦,曲线 BC 、 BDC 都是圆中的弧 , 分别记为 ⌒ 、 ⌒BCBDC弧 BC 这样小于半圆周的圆弧叫做劣弧, 弧 BDC这样大于半圆周的圆弧叫做优弧∠DOB 、∠ BOC 叫圆心角做一做ODBCAE如图,点 A , O , D 以及点 B , O , C分别在一条直线上,则圆中弦的条数为( )A.2 条 B.3 条 C.4 条 D.5 条.OAB圆绕圆心旋转.OAB圆绕圆心旋转.OAB圆绕圆心旋转.OAB圆绕圆心旋转.OAB圆绕圆心旋转.OAB圆绕圆心旋转.OBA圆绕圆心旋转.OBA圆绕圆心旋转.OAB圆绕圆心旋转.OBA180° 所以圆是中心对称图形。圆绕圆心旋转 180° 后仍与原来的圆重合。结论 :OABB'A'在⊙ O 中若∠ B’OA’ =∠ BOA则弦 AB 与弦 A’B’ , AB 与 A’B’有什么关系? ⌒⌒3 、在一个圆中,如果弦相等,那么所对的圆心角相等,圆心角所对的弧 相等。结 论1 、在一个圆中,若圆心角相等,则它所对的弧相等,所对的弦相等。2 、在一个圆中,若弧相等,那么所对的圆心角相等,所对的弦相等。OABB'A'例 题 ⌒ ⌒例 1. 如图,在⊙ O 中 AC=BD, ∠1=45°, 求∠ 2 的度数。 ⌒ ⌒ 解: 因为 AC=BD ⌒ ⌒ ⌒ ⌒ AC-BC=BD-BC ⌒ ⌒ 所以 AB=CD 根据在一个圆中,如果弧相等,那么所对的圆心角相等,可得∠ 2=∠1=45 °DCB21OA练 习 ⌒ ⌒如图,在⊙ O 中, AB=AC, ∠B=70° ,求∠ C 的度数。ABCO3. 如图, AB 、 AC 、 BC 都是⊙ O 的弦,∠ CAB =∠ CBA ,∠COB 与∠ COA 相等吗?为什么? (第 1 题) MOACBN 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。垂径定理垂径定理::①① 已知已知 MNMN 是是⊙⊙ O的直径 ② ② MNAB⊥MNAB⊥比较 AC 与 CB比较 AN 与 NB⌒⌒你有什么发现?MOACBN∵∵MNMN 是是⊙⊙ O 的直径且且 MNAB⊥MNAB⊥垂径定理符号表示:∴AC=BC AM=BMAC=BC AM=BM ⌒⌒ ⌒⌒AN=BNAN=BN⌒⌒