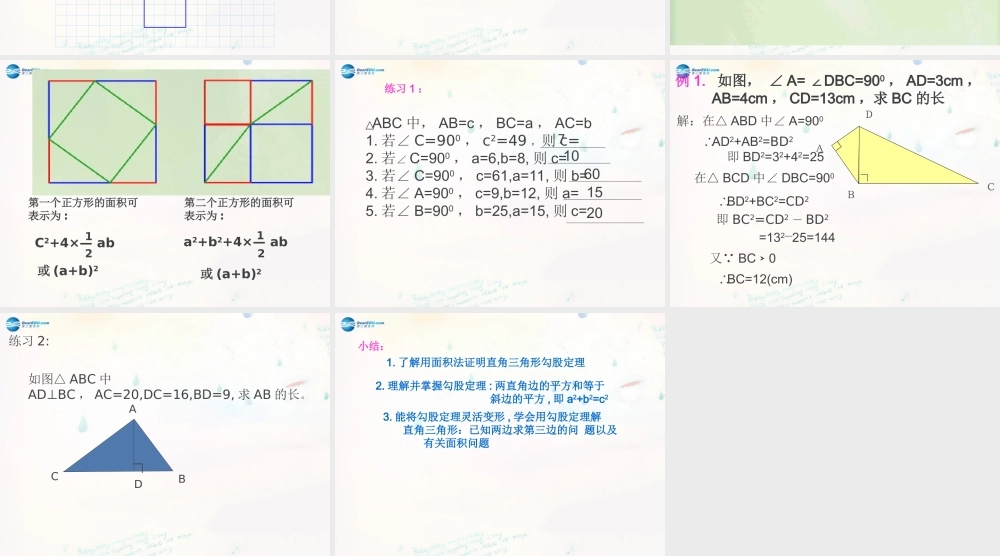
填空:1. 若 a2=36, 则 a= 2. 一个三角形的六要素是指3. 直角三角形三个角中有一个角是直角,两个锐角的关系是 ABC 435 试用三角板画一个直角三角形,使两直角边的长分别为 5cm 和 12cm ,然后用刻度尺去验证一下,这样的直角三角形的斜边的平方是否等于 52+122 ?问题 1.如图△ ABC 中∠ C=900,AC=7cm,BC=4cm, 观察下列图形 ,验证一下 该三角形的斜边长的平方是否等于 42+72? 问题 2.ABC任意的一个直角三角形两直角边长的平方和是否也等于斜边长的平方呢?问题 3 : 第一个正方形的面积可 表示为 :第二个正方形的面积可表示为 :或 (a+b)2或 (a+b)2a2+b2+4×— ab12C2+4×— ab2110601520练习 1 :△ABC 中, AB=c , BC=a , AC=b1. 若∠ C=900 , c2=49 ,则 c=2. 若∠ C=900 , a=6,b=8, 则 c=3. 若∠ C=900 , c=61,a=11, 则 b=4. 若∠ A=900 , c=9,b=12, 则 a=5. 若∠ B=900 , b=25,a=15, 则 c=7例 1. 如图, ∠ A= DBC=90∠0 , AD=3cm , AB=4cm , CD=13cm ,求 BC 的长ADCB∟∟解:在△ ABD 中∠ A=900∴AD2+AB2=BD2 即 BD2=32+42=25在△ BCD 中∠ DBC=900∴BD2+BC2=CD2 =132—25=144又∵ BC0﹥∴BC=12(cm)即 BC2=CD2 - BD2如图△ ABC 中AD⊥BC , AC=20,DC=16,BD=9, 求 AB 的长。ABCD∟练习 2:小结: 1. 了解用面积法证明直角三角形勾股定理 2. 理解并掌握勾股定理 : 两直角边的平方和等于 斜边的平方 , 即 a2+b2=c23. 能将勾股定理灵活变形 , 学会用勾股定理解 直角三角形:已知两边求第三边的问 题以及 有关面积问题