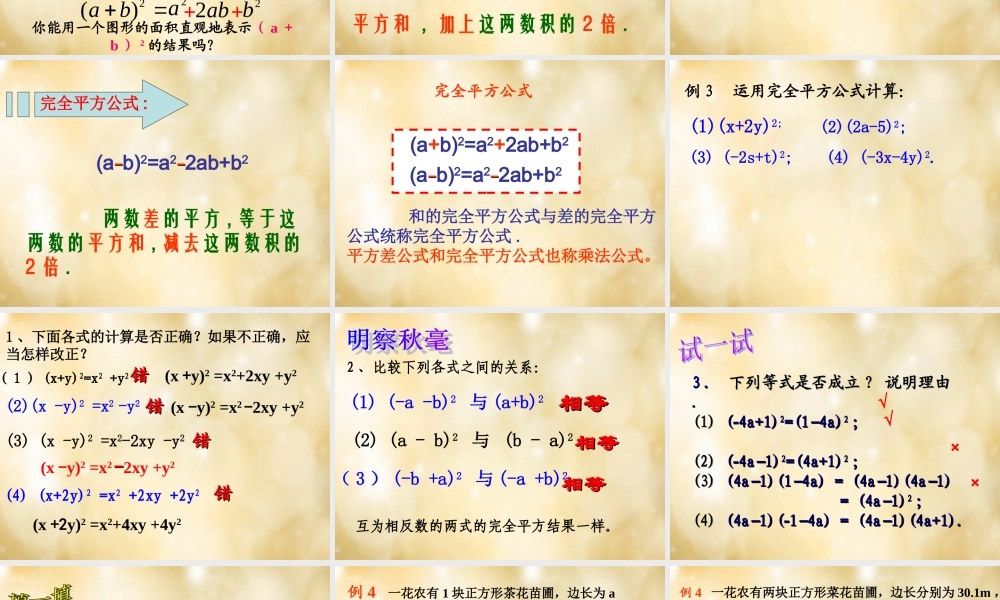
平方差公式 (a+b)(a-b)=a2-b2温故而知新 :两数和与这两数差的积,等于这两数的平方差baab1. (3+4)22= = 3322++4422 ==2. (2+6)22= = 2222++6622 == 49256440(3+4)22 ≠≠ 3322++4422(2+6)22 ≠≠ 2222++6622 运用多项式与多项式相乘的法则计算下列各式:1 、 (a+b)23 、 (2a+x)2 观察上述 1 、 2 两题的计算结果,你发现有什么规律?你能用你的发现来猜测第 3 题的结果吗?=(a+b)(a+b)2 、 (2+x)2 =(2+x)(2+x)= 22+2x+2x+x2=(2a)2+2×2a•x+x2=a2+ab+ab+b2=a2+2ab+b2=22+2×2x+x2bbaa2)(ba(a+b)²a²2ab²2bababab2++完全平方和公式(a+b)(a+b)22== aa22 +2ab+2ab +b +b22 的图形理解你能用一个图形的面积直观地表示( a +b ) 2 的结果吗?完全平方公式 : 两数和的平方 , 等于这两数的平方和 , 加上这两数积的 2 倍 . (a+b)2=a2+2ab+b2小明写出了如下的算式小明写出了如下的算式 ::((aa−−bb))22==[[aa++((−−bb)])]22他是怎么想的他是怎么想的 ?? 你能继续做下去吗你能继续做下去吗 ??aa 2 2 −2−2aabb++bb22..((aa−−bb))22==((aa−−bb))22==[[aa++((−−bb)])]22= = aa22 +2a(-b)+ ( +2a(-b)+ (−−bb))22= = aa22 –2ab+ –2ab+ bb22完全平方公式 : 两数差的平方 , 等于这两数的平方和 , 减去这两数积的2 倍 . (a−−b)2=a2−−2ab+b2 (a+b)2=a2+2ab+b2(a−−b)2=a2−−2ab+b2完全平方公式 和的完全平方公式与差的完全平方公式统称完全平方公式 .平方差公式和完全平方公式也称乘法公式。例 3 运用完全平方公式计算:(1)(x+2y)2; (2)(2a-5)2;(3) (-2s+t)2; (4) (-3x-4y)2.1 、下面各式的计算是否正确?如果不正确,应当怎样改正?(2)(x -y)2 =x2 -y2(3) (x -y)2 =x2-2xy -y2(4) (x+2y)2 =x2 +2xy +2y2错错错错错错错错(x +y)2 =x2+2xy +y2(x -y)2 =x2 -2xy +y2(x -y)2 =x2 --2xy +y2(x +2y)2 =x2+44xy +4y2( 1 ) (x+y)2=x2 +y2(2) (a - b)2 与 (b - a)2 (1) (-a -b)2 与 (a+b)22 、比较下列各式之间的关系:相等相等相等相等( 3 ) (-b +a)2 与 (-a +b)2相等相等互为相反数的两式的完全平方结果一样。33 . . 下列等式是否成立下列等式是否成立 ? ? 说明理由说明理由..(1)(1) ( (4a+1)4a+1)22=(1 4a)−=(1 4a)−22 ; ; (2)(2) ( (4a 1)−4a 1)−22=(4a...