九年级数学下册 圆中比例线段课件人教版 课件VIP免费

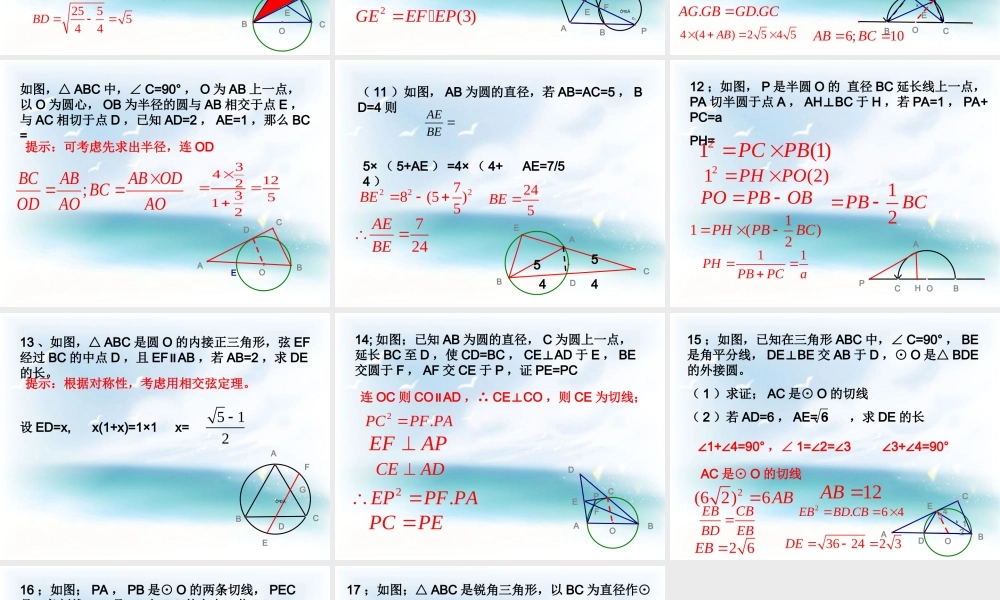
圆中比例线段（ 1 ）相交弦定理如图（ 1 ），若圆内两条弦 AB ， CD 相交于点 P ，则 PA.PB=PC.PD（ 2 ）切割线定理；如图（ 2 ）从圆外一点 A 引圆的切线 AP 和割线 ACB ，则 2.PAAC AB（ 3 ）割线定理；如图（ 3 ）若从圆外一点引圆的两条割线 PAB ， PCD ，则 PA.PB=PC.PDPDCBACBAPCABDP例 1 ；如图 1 ，△ ABC 内接于直径为 d 的圆，设 BC=a ， AC=b ，那么△ ABC 的高 CD=ODCBA连 CO ，并延长 CO 交圆于 E ，连 BE ；Eabd证△ ACDEBC∽△CDbadabCDd例 1 ，如图 2 ， PT 切圆于点 T ， PA 交圆于 A ，B 两点，且与直径 CT 交于点 D ， CD=2 ， AD=3 ，BD=6则 PB=OBDCAPT236？由 3×6=2×TD 可得 TD=922(6?)9PT 2?(9?)PT ? 15如图，在平行四边形 ABCD 中，过 A ， B ， C 三点的圆交 AD 于点 E ，且与 CD 相切，若 AB=4 ，BE=5 ，则 DE 的长为54EDCBAAC=BE=5 ，∠ BAC= ACD= ABC∠∠，则 AC=BC=AD=5 ， DC=AB=4DE= 165连 AC ， CE例 3 ；如图，已知圆是三角形 ABC 的外接圆， BC是圆的直径， D 是劣弧 的中点， DB 交 AC 于点 E2(1).55,,22ADDE DBBCCDDE求证若求的长jOEDCBA由 AD.AD=DE.DB; 得 ADDBDEAD证△ ADEBDA∽△255544BD 25.4ADDE DBDE得例如图， P 是平行四边形 ABCD 的边 AB 的边 AB的延长线上一点， DP 与 AC ， BC 分别交于点 E ，F ，EG 是过 B ， F ， P 三点圆的切线， G 为切点，求证EG=DEc1FEGCDPBAÔ²ÐÄ(1)CEEFAEDE(2)CEDEAEEP2(3)GEEF EP由（ 1 ）（ 2 ）知2DEEF EP例 5 如图， BC 是半圆 O 的直径， D 是 的中点，四边形 ABCD 的对角线 AC ， BD 交于点 E ，（ 1 ）求 AC. BC=2BD.CD;(2)AE=3,CD=2 , 求弦 AB 和直径 BC 的长kEODCBA（ 1 ） BC=2OB AC.OB=BD.CD∴ACBDCDBO证△ BDOACD∽△（ 2 ）延长 CD ， BA 交于 G ，证△ CDECAG∽△G2 5534 5CECDCECECGACCE22(4 5)84AG ..AG GBGD GC4 (4)2 54 5AB6;10ABBC如图，△ ABC 中，∠ C=90° ， O 为 AB 上一点，以 O 为圆心， OB 为半径的圆与 AB 相交于点 E ，与 AC 相切于点 D ，已知 AD=2 ， AE=1 ，那么 BC=ODCBA;BCABAB O...