八年级数学下册 19.3一元二次方程的根的判别式课件 沪科版 课件VIP免费

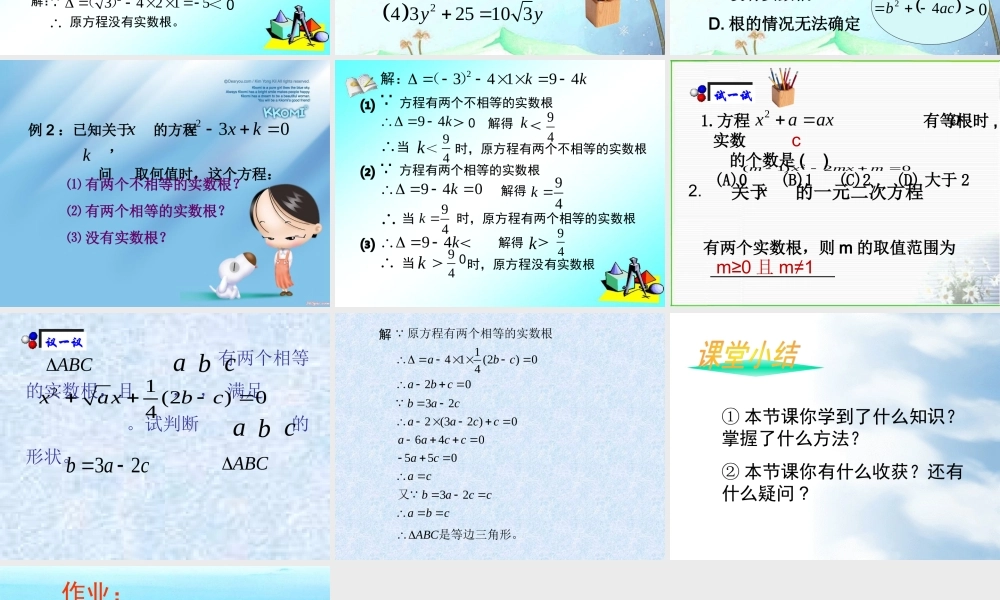
19.3 一元二次方程的根的判别式    2221 53202 254203 2310xxyyxx 利用公式法解下列方程 对于一元二次方程你能谈论一下它的根的情况吗 ?在什么情况下，一元二次方程有解 ? 有什么样的解 ?什么情况下一元二次方程无解 ?20(0)axbxca想一想想一想    2221 53202 254203 2310xxyyxx  例 1. 不解方程，判别下列方程的根的情况。  21 5320xx解： 2225420yy234 5249    （）（）＞ 0 原方程有两个不相等的实数根。解：原方程可变形为2252040yy2204 25 40   （） 原方程有两个相等的实数根。 23 2310xx 解：234 2 15   （）＜ 0 原方程没有实数根。 1. 不解方程，判别下列方程的根的情况。    2221 25402 75203(1)34 32510 3xxttx xyy练一练练一练 2. 在一元二次方程中)0(02acbxax则方程异号与若,ca （ ）A. 有两个不相等的实数根B. 有两个相等的实数根C. 没有实数根D. 根的情况无法确定acb42 acb420A 例 2 ：已知关于 的方程 ， 问 取何值时，这个方程： 230xxk⑴ 有两个不相等的实数根？⑵ 有两个相等的实数根？⑶ 没有实数根？kx 解：234 194kk     （）⑴94k  ＞ 0 方程有两个不相等的实数根k＜ 94＜ 94k时，原方程有两个不相等的实数根⑵940k   方程有两个相等的实数根94k 94k 时，原方程有两个相等的实数根⑶94k  ＜ 0＞ 94＞ 94k时，原方程没有实数根k解得当解得当解得当 1.方程 有等根时 ,实数 的个数是 ( ) (A)0 (B)1 (C)2 (D) 大于 22xaaxa2. 关于 的一元二次方程 2(1)20mxmxmm≥0 且 m≠1x有两个实数根，则 m 的取值范围为c试一试试一试 设 的三边为 ， ， ，方程 有两个相等的实数根，且 ， ， 满足 。试判断 的形状。 ABCa b c21 (2)04xaxbca b c32bacABC议一议议一议 14 1(2)0420abcabc     原方程有两个相等的实数根322 (32 )0640550bacaaccaaccacac 32baccabc 又ABC是等边三角形。解 ① 本节课你学到了什么知识？掌握了什么方法？② 本节课你有什么收获？还有什么疑问 ? 作业： 课本第 53 面第 1 ， 2 ， 3 ，5 题