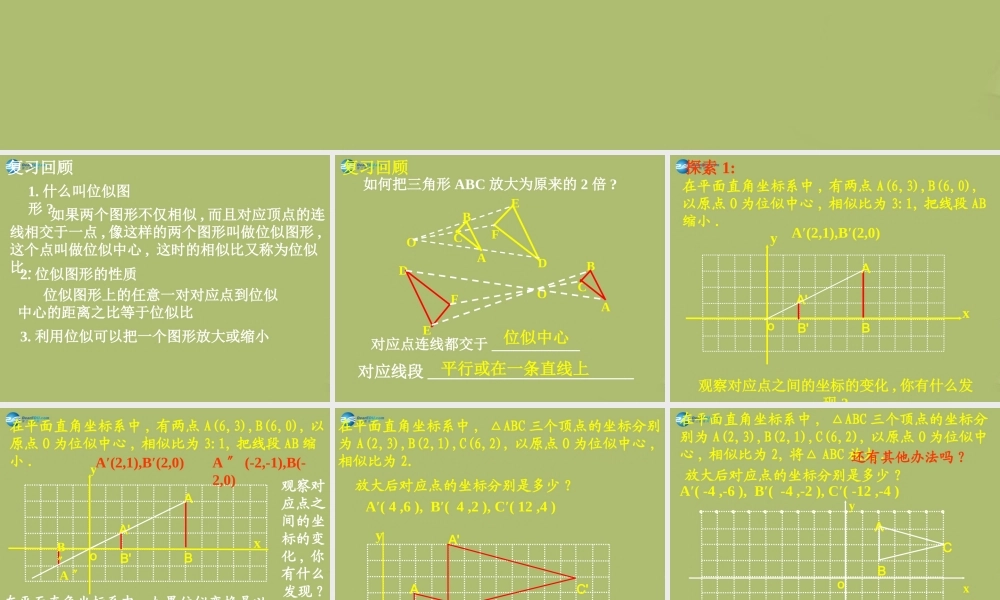
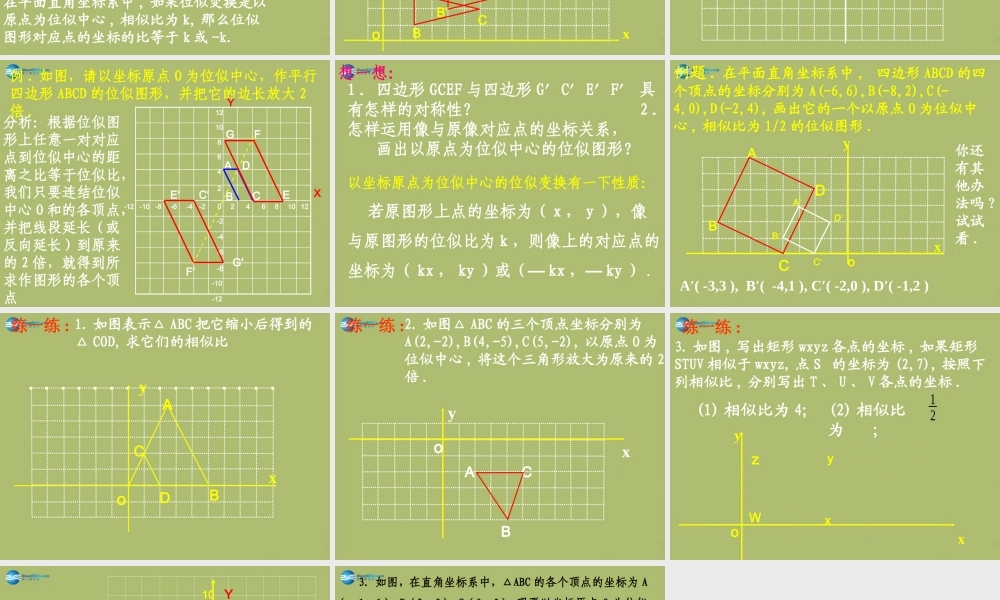
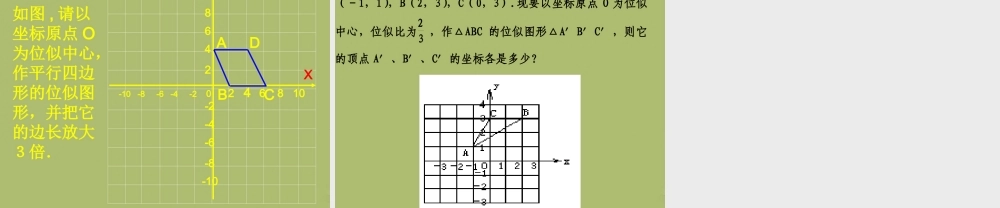
27.3 位似 如果两个图形不仅相似 , 而且对应顶点的连线相交于一点 , 像这样的两个图形叫做位似图形 , 这个点叫做位似中心 , 这时的相似比又称为位似比 .1. 什么叫位似图形 ?2. 位似图形的性质 位似图形上的任意一对对应点到位似中心的距离之比等于位似比3. 利用位似可以把一个图形放大或缩小复习回顾DEFAOBC如何把三角形 ABC 放大为原来的 2 倍 ?DEFAOBC对应点连线都交于 ____________对应线段 _________________________位似中心平行或在一条直线上复习回顾B'A'xyBAo在平面直角坐标系中 , 有两点 A(6,3),B(6,0),以原点 O 为位似中心 , 相似比为 3:1, 把线段 AB缩小 .A′(2,1),B′(2,0)观察对应点之间的坐标的变化 , 你有什么发现 ?探索 1:B'A'xyBAo在平面直角坐标系中 , 有两点 A(6,3),B(6,0), 以原点 O 为位似中心 , 相似比为 3:1, 把线段 AB 缩小 .A′(2,1),B′(2,0)A 〞B〞A 〞 (-2,-1),B(-2,0)在平面直角坐标系中 , 如果位似变换是以原点为位似中心 , 相似比为 k, 那么位似图形对应点的坐标的比等于 k 或 -k.观察对应点之间的坐标的变化 , 你有什么发现 ?xyo在平面直角坐标系中 , △ABC 三个顶点的坐标分别为 A(2,3),B(2,1),C(6,2), 以原点 O 为位似中心 ,相似比为 2.BACA′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )放大后对应点的坐标分别是多少 ?B'A'C'xyo在平面直角坐标系中 , △ABC 三个顶点的坐标分别为 A(2,3),B(2,1),C(6,2), 以原点 O 为位似中心 , 相似比为 2, 将△ ABC 放大 .A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )BAC放大后对应点的坐标分别是多少 ?还有其他办法吗 ?E′例 . 如图,请以坐标原点 O 为位似中心,作平行四边形 ABCD 的位似图形,并把它的边长放大 2倍 . XY-2246-6-48-8-101012-12DABC124026810-2-4-6-8-10-12分析:根据位似图形上任意一对对应点到位似中心的距离之比等于位似比,我们只要连结位似中心 O 和的各顶点,并把线段延长(或反向延长)到原来的 2 倍,就得到所求作图形的各个顶点 GFEC′G′F′以坐标原点为位似中心的位似变换有一下性质: 若原图形上点的坐标为( x , y ),像与原图形的位似比为 k ,则像上的对应点的坐标为( kx , ky )或(― kx ,― ky ) . 想一想:1 .四边形 GCEF 与四边形 G′C′E′F′ 具有怎样的对称性? 2 ....