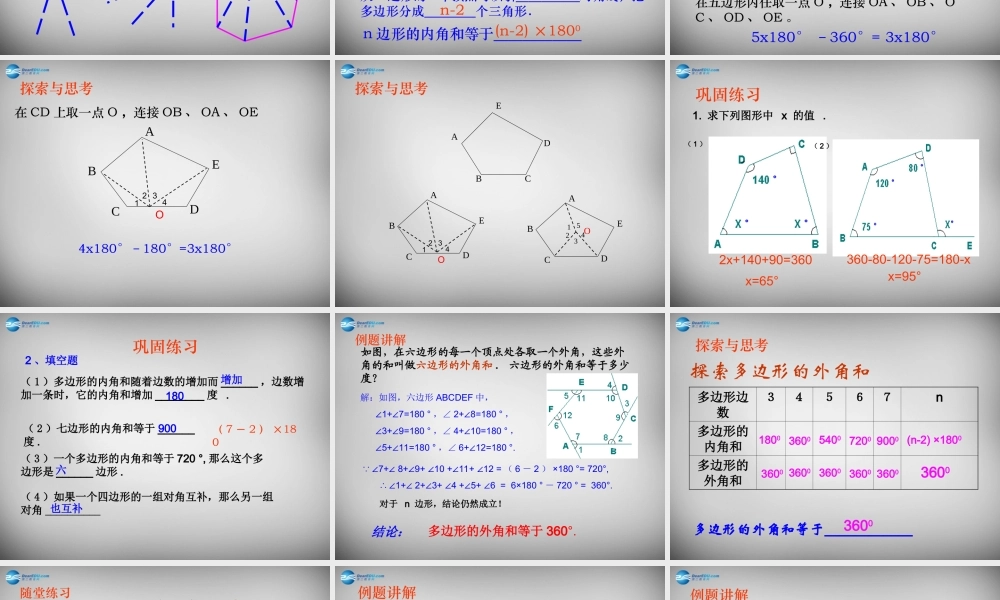
11.3.2 多边形的内角和(1) 掌握多边形的内角和的计算方法,并能用内角和知识解决一些较简单的问题;(2) 通过多边形内角和的计算公式的推导,培养探索和归纳的能力;(3) 体验转化的数学思想方法。学习目标重点与难点:(1) 重点 : 多边形内角和以及外角和;(2) 难点 : 多边形内角和以及外角和的推导。3、三角形的内角和是 _____ 度.2、在多边形中连接 ______________________的线段叫做多边形的对角线。1 、在平面内, ___________________________ 叫做多边形。由一些线段首尾顺次相接组成的图形多边形不相邻的两个顶点1804 、正方形的内角和是 度,长方形的内角和是 度。36003600知识回顾ABCD任意一个四边形的内角和都等于 360°思路:把求四边形内角和的问题转化为三角形问题来解决!想一想:一般的四边形的内角和是多少度呢五边形的内角和为 540 0七边形的内角和为 900 0六边形的内角和为 720 0四边形、五边形、六边形、七边形从一个顶点出发分别可以引多少条对角线?分别把多边形分成多少个三角形?你能从中探索出规律吗?试求五边形、六边形、七边形的内角和.探索与思考多边形边数 34567n从一个顶点引对角线的条数分成的三角形个数多边形的内角和n-24321054321n-31800 3600 5400 7200 9000 (n-2) ×1800从 n 边形的一个顶点可以引_____对角线,把多边形分成____个三角形.n 边形的内角和等于______n-3n-2(n-2) ×1800探索与思考 完成下表AEDCBO1 54325x180° –360°= 3x180°在五边形内任取一点 O ,连接 OA 、 OB 、 OC 、 OD 、 OE 。探索与思考除了上述我们利用对角线,将一个多边形分割成几个三角形外,还有其它的分割方法吗AEDCBO12 344x180°–180°=3x180°在 CD 上取一点 O ,连接 OB 、 OA 、 OE探索与思考AEDCBO1 5432AEDCBO12 34ABCDE探索与思考1. 求下列图形中 x 的值 .( 1 )( 2 )巩固练习2x+140+90=360360-80-120-75=180-xx=65°x=95°( 2 )七边形的内角和等于 ______度 .2 、填空题900( 7 - 2 ) ×180( 3 )一个多边形的内角和等于 720 °, 那么这个多边形是 ______ 边形 .六( 4 )如果一个四边形的一组对角互补,那么另一组对角 __________也互补( 1 )多边形的内角和随着边数的增加而 ______ ,边数增加一条时,它的内角和增加 ________ 度 .增加180巩固练习如图,在六边形的...