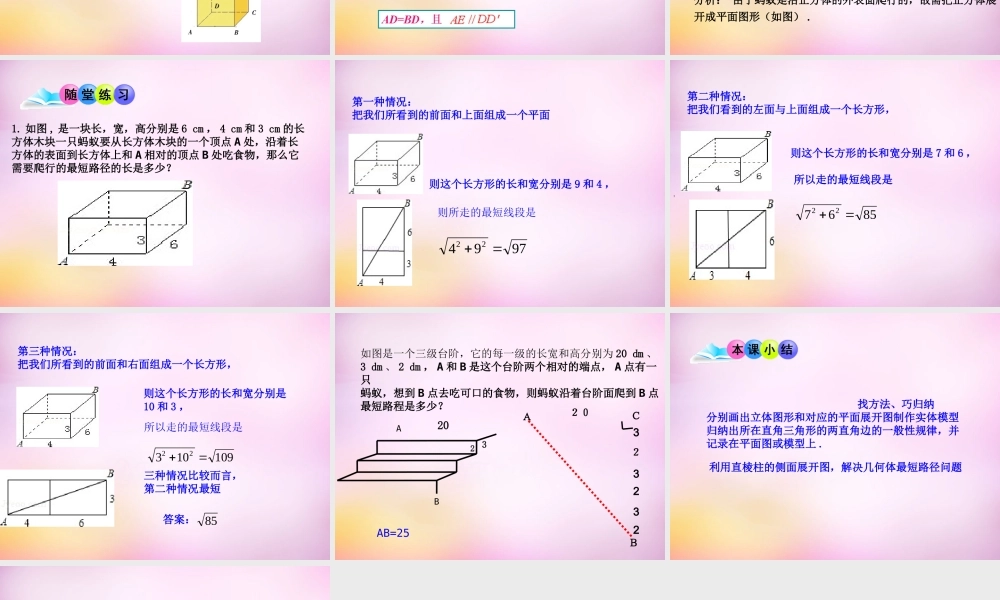
7.2 直棱柱的侧面展开图 第 2 课时 1. 了解直棱柱的侧面展开图和表面展开图,能根据展开图想象所描述的实际物体。2. 利用直棱柱的侧面展开图知识,计算直棱柱的侧面积和表面积及解决一些实际问题。多面体棱柱直棱柱斜棱柱几种多面体的相互关系1. 将三个都相邻的面上做有标记的立方体盒子展开,以下各示 意图中有可能是它的展开图的是( )ABCDC例题 一只苍蝇停落在一个无盖的棱长为 1 m 的立方体形箱子的顶点 D ′ 处 . 藏在箱子底部的点 B 处的一只蜘蛛发现了这只苍蝇 .( 1 )如果蜘蛛沿着 BB ′ —B′ A ′—A ′ D ′ 的路径去捕捉苍蝇,需要爬行多少路程?( 1 )如果蜘蛛沿着 BA ′ —A ′ D ′ 的路径去捕捉苍蝇,需要爬行多少路程?( 3 )蜘蛛沿箱子内壁上的哪条路径去捕捉苍蝇,爬行的路程最短?最短路径是多少?( 3 )如图是一个箱子的侧面展开图,连接 BD′ 则 BD′ 的长为展开图中的最短距离,也是蜘蛛沿箱子内壁,由 B 点爬到 D′ 点的最短距离,此时, BD′ 与 AC 的交点恰为 AA′ 的中点B’A’C’D’CBD如图,边长为 1 的正方体中,一只蚂蚁从顶点 A 出发沿着正方体的外表面爬到顶点 B 的最短距离是( ) . ( A ) 3 ( B ) 5 ( C ) 2 ( D ) 1AB分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图) .CABC21B√1. 如图 , 是一块长,宽,高分别是 6 cm , 4 cm 和 3 cm 的长方体木块一只蚂蚁要从长方体木块的一个顶点 A 处,沿着长方体的表面到长方体上和 A 相对的顶点 B 处吃食物,那么它需要爬行的最短路径的长是多少? 则这个长方形的长和宽分别是 9 和 4 ,则所走的最短线段是第一种情况:把我们所看到的前面和上面组成一个平面979422则这个长方形的长和宽分别是 7 和 6 ,所以走的最短线段是 ;第二种情况:把我们看到的左面与上面组成一个长方形,85672210910322则这个长方形的长和宽分别是10 和 3 ,所以走的最短线段是三种情况比较而言,第二种情况最短 答案:第三种情况:把我们所看到的前面和右面组成一个长方形,85如图是一个三级台阶,它的每一级的长宽和高分别为 20 dm 、3 dm 、 2 dm , A 和 B 是这个台阶两个相对的端点, A 点有一只蚂蚁,想到 B 点去吃可口的食物,则蚂蚁沿着台阶面爬到 B 点最短路程是多少?2032AB20232323ABCAB=25利用直棱柱的侧面展开图,解决几何体最短路径问题 找方法、巧归纳分别画出立体图形和对应的平面展开图制作实体模型归纳出所在直角三角形的两直角边的一般性规律,并记录在平面图或模型上 .