三垂线定理及其逆定理 江苏省高二数学立体几何直线与平面单元全部系列课件 人教版 江苏省高二数学立体几何直线与平面单元全部系列课件 人教版VIP免费

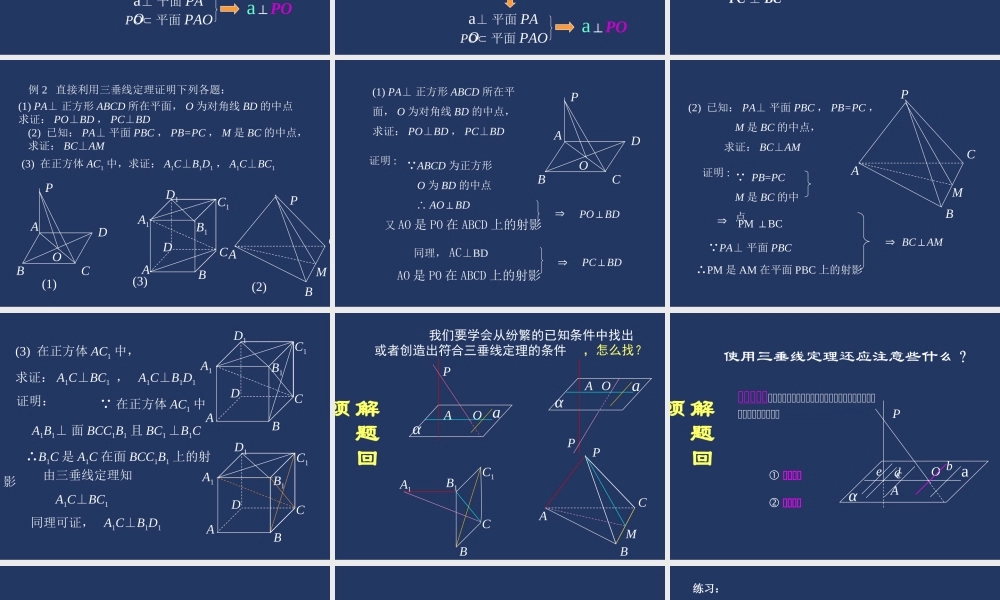
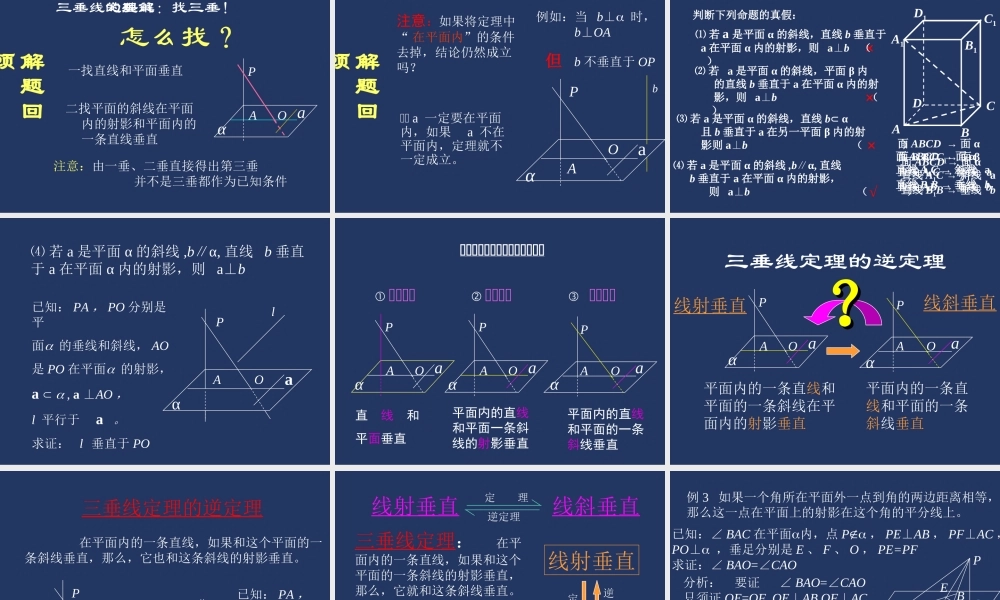
三垂线定理及其逆定理 一、复习回顾：空间中两条直线的位置关系有哪几种？如何判定两条异面直线互相垂直呢？1 、定义法2 、直线与平面垂直的性质 : 线面垂直 , 则线线垂直 EMDBOAAE⊥OD？cos·cos=cos=AOB∠ =AOD∠ =DOB∠AaOPPO ⊥ a？ AaOP 已知 PA 、 PO 分别是平面的垂线、斜线， AO 是 PO在平面上的射影。 a  ， a⊥AO 。求证： a⊥PO在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么，它就和这条斜线垂直。三垂线定理二、新授： AaOP证明：a⊥POPA⊥ a  AO⊥aa⊥ 平面 PAOPO 平面 PAOPA ⊥a 三垂线定理 ：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么，它就和这条斜线垂直。AaOPa⊥POPA⊥ a  AO⊥aa⊥ 平面 PAOPO 平面 PAOPA ⊥a证明： PCBAO例 1 已知 P 是平面 ABC 外一点， PA⊥ 平面 ABC ， AC ⊥ BC ， 求证： PC ⊥ BC证明： P 是平面 ABC 外一点 PA⊥ 平面 ABC ∴PC 是平面 ABC 的斜线 ∴AC 是 PC 在平面 ABC 上的射影 BC 平面 ABC 且 AC ⊥ BC ∴ 由三垂线定理得 PC ⊥ BCM 例 2 直接利用三垂线定理证明下列各题：(1) PA⊥ 正方形 ABCD 所在平面， O 为对角线 BD 的中点求证： PO⊥BD ， PC⊥BD(3) 在正方体 AC1 中，求证： A1C⊥B1D1 ， A1C⊥BC1(2) 已知： PA⊥ 平面 PBC ， PB=PC ， M 是 BC 的中点，求证： BC⊥AMA D C B A1D1B1C1(1)(3)BPMCA(2)POABCD (1) PA⊥ 正方形 ABCD 所在平面， O 为对角线 BD 的中点，求证： PO⊥BD ， PC⊥BDPOABCD证明 : ABCD 为正方形 O 为 BD 的中点 ∴ AO⊥BD又 AO 是 PO 在 ABCD 上的射影PO⊥BD 同理， ACBD⊥ AO 是 PO 在 ABCD 上的射影PC⊥BD PMCAB(2) 已知： PA⊥ 平面 PBC ， PB=PC ， M 是 BC 的中点， 求证： BC⊥AMBC⊥AM证明 : PB=PCM 是 BC 的中点PM BC⊥ PA⊥ 平面 PBC∴PM 是 AM 在平面 PBC 上的射影 (3) 在正方体 AC1 中，求证： A1C⊥BC1 ， A1C⊥B1D1 在正方体 AC1 中 A1B1⊥ 面 BCC1B1 且 BC1 ⊥B1C ∴B1C 是 A1C 在面 BCC1B1 上的射影 C B A1B1 C1A D D1证明： C B A1B1 C1A D D1同理可证， A1C⊥B1D1由三垂线定理知...