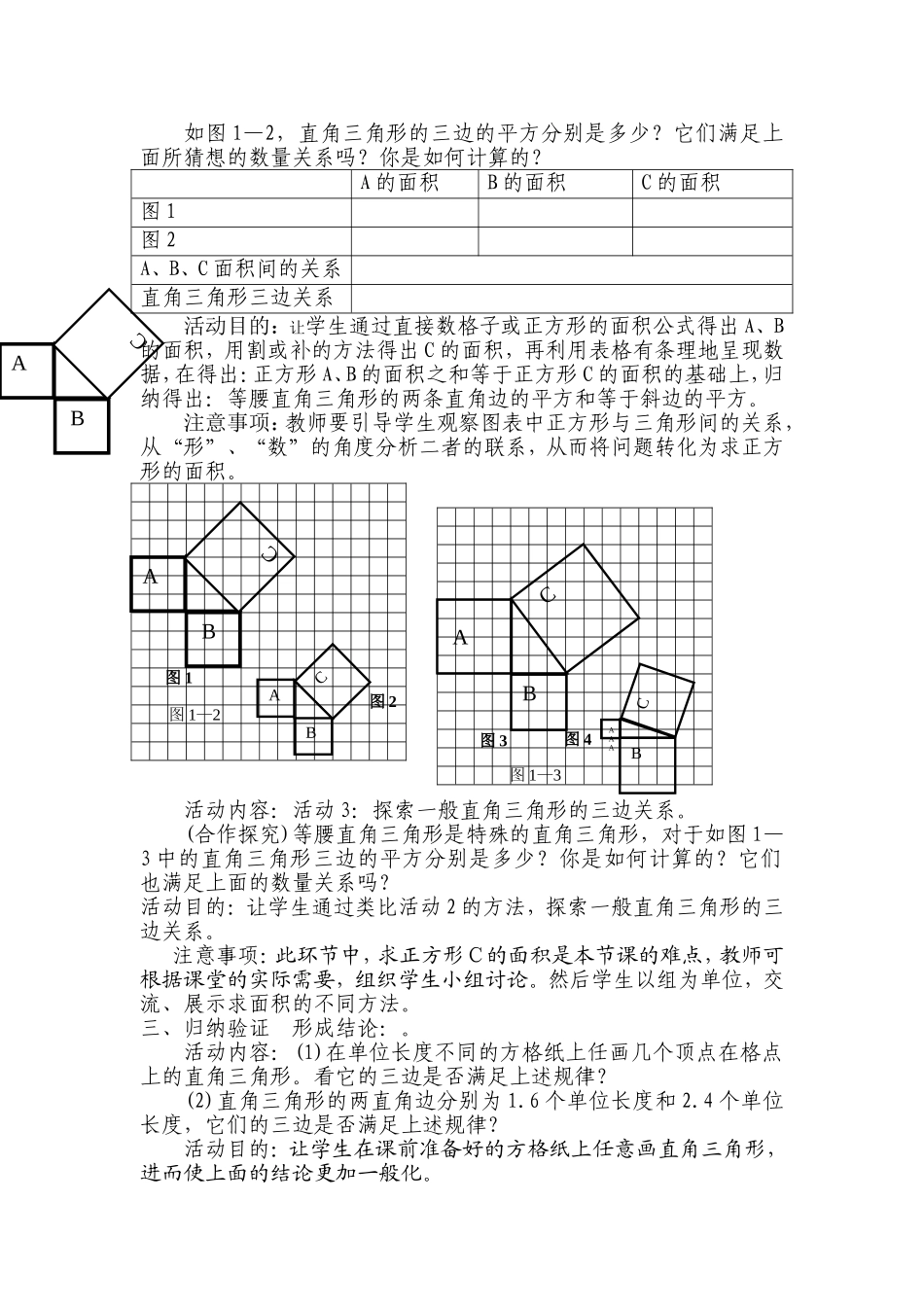
《勾股定理(一)》教学设计 教学目标(1)、经历用数格子的办法探索勾股定理的过程,进一步发展学生合情推理意识,体会数学与现实生活的紧密联系。(2)、能说出勾股定理的内容并会初步运用勾股定理进行简单的计算和实际运用。(3)、在探索勾股定理的过程中,让学生经历“观察-猜想-归纳-验证”的探究过程,并体会由特殊到一般、数形结合以及转化的思想方法。(4)、在探究活动中,培养学生独立思考、合作交流的学习习惯,通过解决实际问题,增强自信心,激发学习数学的兴趣在教师的介绍下,体会勾股定理的文化价值。教学重点:勾股定理的发现、探索过程。教学难点:将边不在格线上的图形转化边在格线上的图形,以便于计算图形的面积。课前准备:方格纸、课件教学过程:一、创设情景 导入新课:活动内容:情境一:情境 1:出示章前图,通过“怎样与外星人联系”的话题激发学生的探究欲望,明确本章的学习内容。情境二:如图,强大的台风使的一根旗杆在离地面 9 米处断裂,旗杆顶部落在离旗杆底部 12 米处。旗杆折断之前有多高? 想一想:你需要求哪些线段长度,这些长度确定吗?活动目的:教师引导学生把实际问题转化成数学问题,也就是“已知直角三角形的两边,如何求第三边?”的问题。再结合“想一想”中的问题,让学生认识到在直角三角形中,任意两边确定了,另外一条边也就随之确定了,三条边之间确实存在一个特定的数量关系,从而引出对直角三角形三边关系的探索。注意事项:学生能够获取信息,但对于直角三角形中已知任意两边,第三边也就随之确定了理解比较困难,教师可让学生尝试画图并充分的交流自己的想法。二、尝试猜想 探索验证:活动内容:活动 1:尝试猜想在纸上任意画若干个直角三角形,测量它们各边的长度,看看三边长的平方有什么关系?活动目的:让学生画直角三角形,通过测量得出结论,猜想出了直角三角形三边长平方的关系注意事项:在学生画直角三角形测量时,教师要适当给予帮助,尽可能的减小误差。活动内容:活动 2:探索特殊直角三角形的三边关系。 912图 1—2A B CA B CBA C AB CBAAA C图 1—3如图 1—2,直角三角形的三边的平方分别是多少?它们满足上面所猜想的数量关系吗?你是如何计算的?A 的面积B 的面积C 的面积图 1图 2A、B、C 面积间的关系直角三角形三边关系活动目的:让学生通过直接数格子或正方形的面积公式得出 A、B的面积,用割或补的方法得出 C 的面积,再利用表格有...