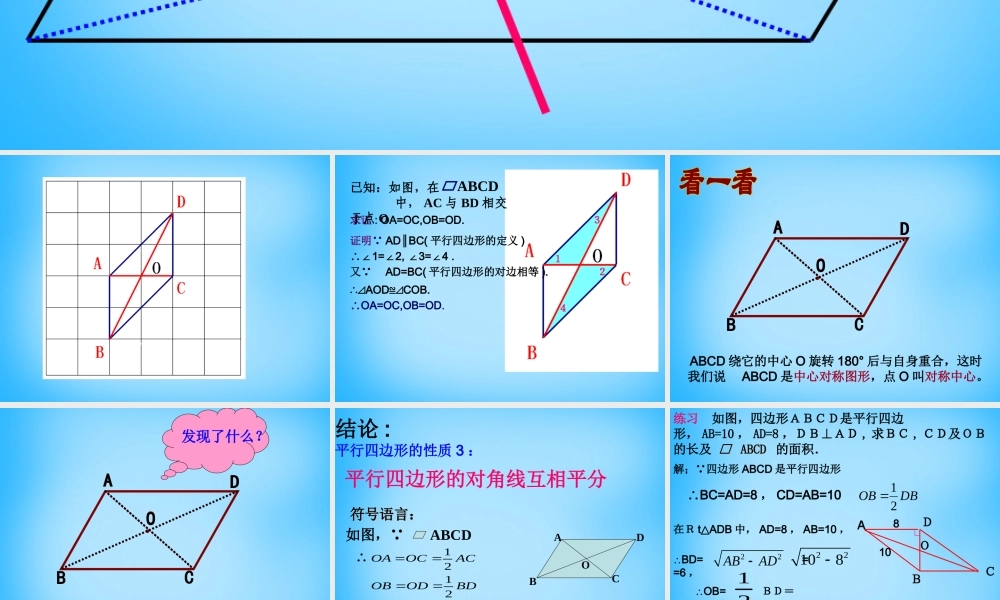
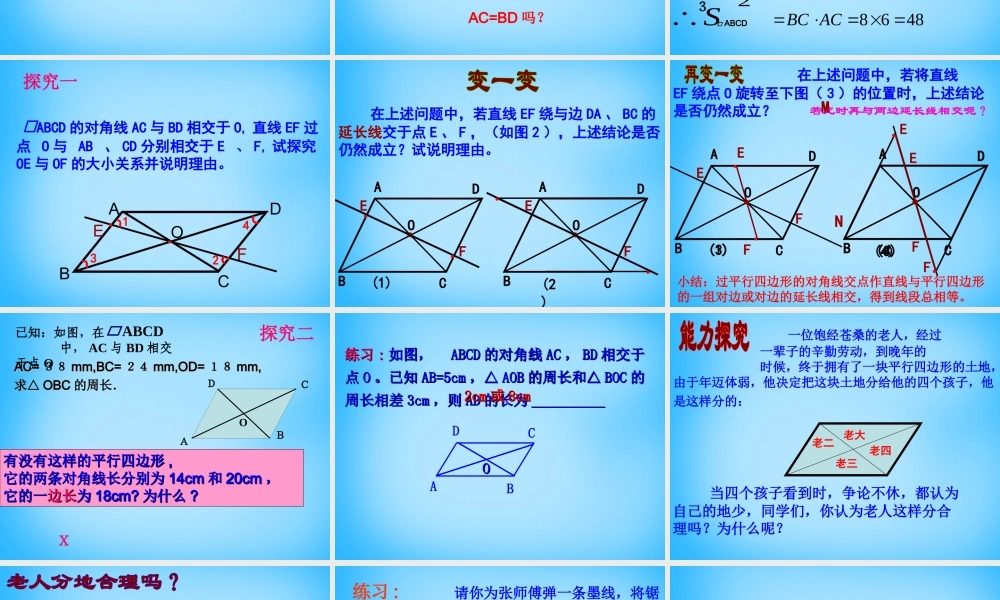
19.1.119.1.1 平行四边形的性质平行四边形的性质 (( 第二课时第二课时 ))4123求证 : OA=OC,OB=OD.证明 AD BC(∥平行四边形的定义 )∴∠1=2, 3=4 .∠∠∠又 AD=BC( 平行四边形的对边相等 ).∴⊿AODCOB.≌⊿∴OA=OC,OB=OD.已知:如图,在 中, AC 与 BD 相交于点 OABCD●ADOCBDBOCA ABCD 绕它的中心 O 旋转 180° 后与自身重合,这时我们说 ABCD 是中心对称图形,点 O 叫对称中心。 ●ADOCBDBOCA发现了什么?平行四边形的对角线互相平分结论 :平行四边形的性质 3 :AC=BD 吗?ODCBABDODOBACOCOA2121如图, ABCD 符号语言:符号语言:∴练习 如图,四边形ABCD是平行四边形, AB=10 , AD=8 ,DB⊥AD , 求BC , CD及OB的长及 □ □ ABCDABCD 的面积.CABDO810∟解; 四边形 ABCD 是平行四边形12∴OB= BD=32210822ABAD∴BD= = =6 ,在R t ADB△中, AD=8 , AB=10 ,∴BC=AD=8 , CD=AB=10S□ □ ABCDABCD4868ACBCDBOB21 ABCD 的对角线 AC 与 BD 相交于 O, 直线 EF 过点 O 与 AB 、 CD 分别相交于 E 、 F, 试探究OE 与 OF 的大小关系并说明理由。ABCDOEF●●●1234探究一●ODCBAEF●ODCBAEF(1)(2) 在上述问题中,若直线 EF 绕与边 DA 、 BC 的延长线交于点 E 、 F ,(如图 2 ),上述结论是否仍然成立?试说明理由。●●●● 在上述问题中,若将直线 EF 绕点 O 旋转至下图( 3 )的位置时,上述结论是否仍然成立?FEF●ODCBAE(1)●ODCBAEF(3)(3)(4)若此时再与两边延长线相交呢?●ODCBAEF(4)MN●●●●小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。AC=AC= 3838 mm,BC=mm,BC= 2424 mm,OD=mm,OD= 1818 mm,mm,求△求△ OBCOBC 的周长.的周长.CBAODX有没有这样的平行四边形有没有这样的平行四边形 ,,它的两条对角线长分别为它的两条对角线长分别为 14cm14cm 和和 20cm20cm ,,它的一它的一边长边长为为 18cm?18cm? 为什么为什么 ??已知:如图,在 中, AC 与 BD 相交于点 OABCD探究二练习练习 :: 如图, 如图, ABCDABCD 的对角线的对角线 ACAC ,, BDBD 相交于相交于点点 OO 。已知。已知 AB=5cmAB=5cm ,△,△ AOBAOB 的周长和△的周长和△ BOCBOC ...