反函数 函数第二章高三数学文科第一轮复习课件全集 新课标 人教版 函数第二章高三数学文科第一轮复习课件全集 新课标 人教版VIP免费

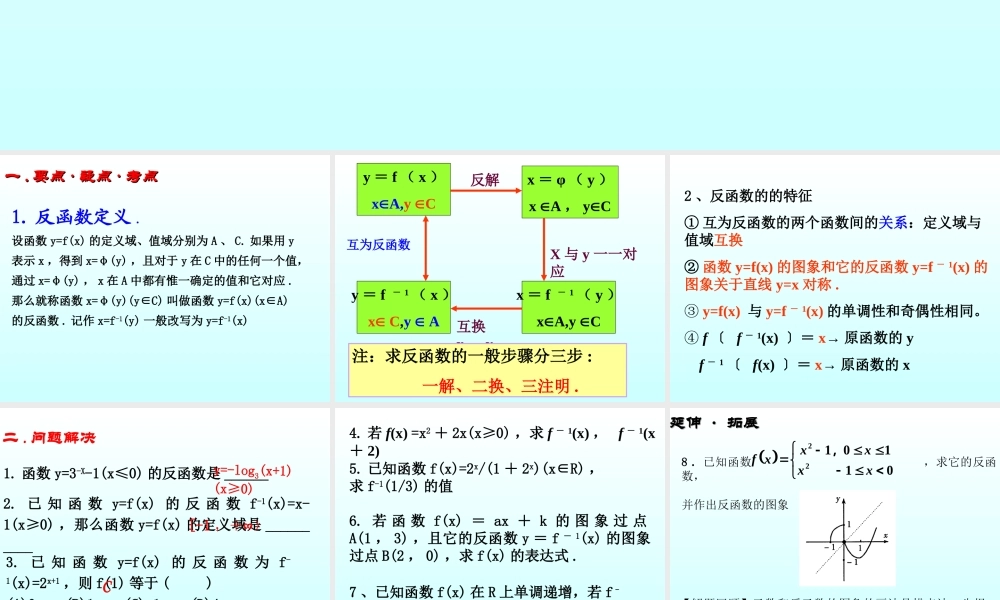
1. 反函数定义 .设函数 y=f(x) 的定义域、值域分别为 A 、 C. 如果用 y表示 x ，得到 x=φ(y) ，且对于 y 在 C 中的任何一个值，通过 x=φ(y) ， x 在 A 中都有惟一确定的值和它对应 .那么就称函数 x=φ(y)(y∈C) 叫做函数 y=f(x)(x∈A)的反函数 . 记作 x=f-1(y) 一般改写为 y=f-1(x)一一 .. 要点要点 ·· 疑点疑点 ·· 考点考点y ＝ f （ x ）xA,y Cx ＝ φ （ y ）x A ， yCy ＝ f － 1 （ x ）x C,y  Ax ＝ f － 1 （ y ）xA,y C反解X 与 y 一一对应互换x ， y互为反函数注：求反函数的一般步骤分三步 : 一解、二换、三注明 .2 、反函数的的特征① 互为反函数的两个函数间的关系：定义域与值域互换② 函数 y=f(x) 的图象和它的反函数 y=f － 1(x) 的图象关于直线 y=x 对称 . ③ y=f(x) 与 y=f － 1(x) 的单调性和奇偶性相同。 ④ f 〔 f － 1(x) 〕＝ x→ 原函数的 y f － 1 〔 f(x) 〕＝ x→ 原函数的 x二 . 问题解决1. 函数 y=3-X-1(x≤0) 的反函数是 ______2. 已 知 函 数 y=f(x) 的 反 函 数 f-1(x)=x-1(x≥0) ，那么函数 y=f(x) 的定义域是 __________y=-log3(x+1)(x≥0)[-1∞，＋ ）3. 已 知 函 数 y=f(x) 的 反 函 数 为 f-1(x)=2x+1 ，则 f(1) 等于 ( ) (A)0 (B)1 (C)-1 (D)4 C4. 若 f(x) =x2 ＋ 2x(x≥0) ，求 f － 1(x) ， f － 1(x＋ 2) 5. 已知函数 f(x)=2x/(1 ＋ 2x)(x∈R) ，求 f-1(1/3) 的值6. 若 函 数 f(x) ＝ ax ＋ k 的 图 象 过 点A(1 ， 3) ，且它的反函数 y ＝ f － 1(x) 的图象过点 B(2 ， 0) ，求 f(x) 的表达式 .7 、已知函数 f(x) 在 R 上单调递增，若 f–1(a+1)