数学 3.2.3立体几何中的向量方法 距离课件 新人教A版选修2 1 课件VIP免费

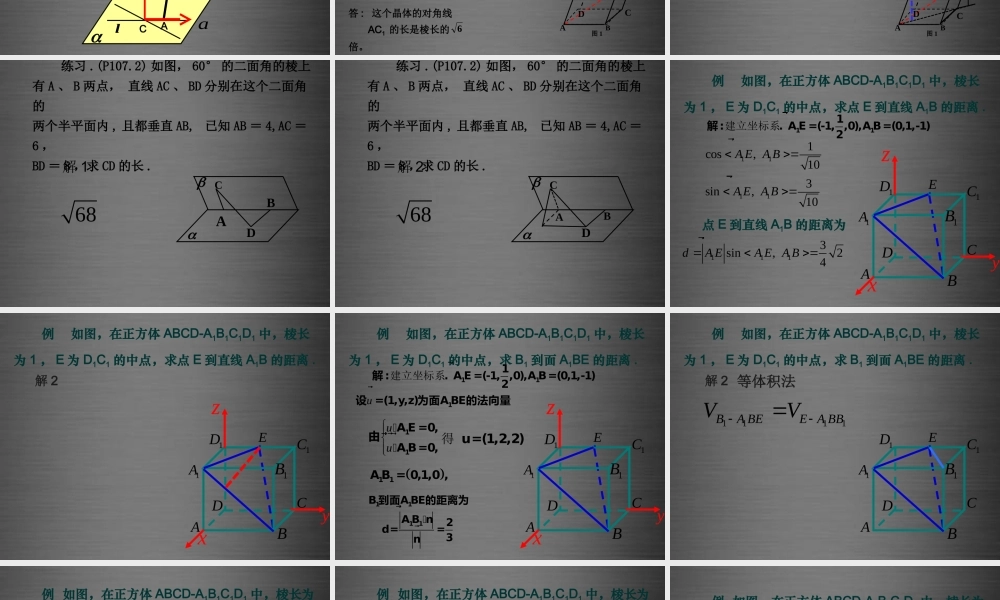
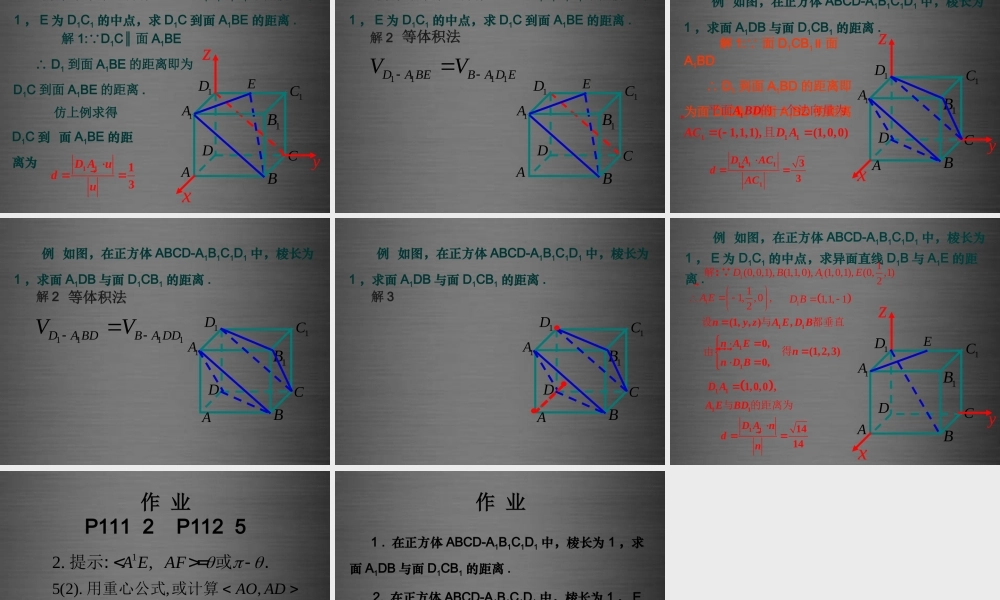
3.2.3 立体几何中的向量方法—— 距离问题距离问题：设直线 l,m 的方向向量分别为 ,a b， 平面,  的法向量分别为 ,u v，则 (1) A(x1,y1,z1), B(x2,y2,z2), 则�222121212AB = (x -x ) +(y -y ) +(z -z )距离问题：设直线 l,m 的方向向量分别为 ,a b， 平面,  的法向量分别为 ,u v，则 a�d= AP sin(2) 点 P 与直线 l 的距离为 d , 则距离问题：设直线 l,m 的方向向量分别为 ,a b， 平面,  的法向量分别为 ,u v，则 (3) 点 P 与平面 α 的距离为 d , 则uAPOdd=| AP�| |cos AP, u�|=||||AP uu��. 距离问题：设直线 l,m 的方向向量分别为 ,a b， 平面,  的法向量分别为 ,u v，则 (4) 平面 α 与 β 的距离为 d , 则umDCPAlabd=| AP�| |cos AP, u�|=||||AP uu��. 例 1 如图 1 ：一个结晶体的形状为四棱柱，其中，以顶点 A 为端点 的三条棱长都相等，且它们彼此的夹角都是 60° ，那么以这 个顶点为端点的晶体的对角线的长与棱长有什么关系？ A1B1C1D1ABCD 图 1解：如图 1 ，1111 60ABAAADBADBAADAA设，11AAADABAC2121)(AAADABAC)(2112122AAADAAABADABAAADAB)60cos60cos60(cos21116所以6||1 AC答 : 这个晶体的对角线 AC1 的长是棱长的 倍。6 例 1 如图 1 ：一个结晶体的形状为四棱柱，其中，以顶点 A 为端点 的三条棱长都相等，且它们彼此的夹角都是 60° ，那么以这 个顶点为端点的晶体的对角线的长与棱长有什么关系？ A1B1C1D1ABCD 图 1解 2 ：如图1 ，1111 60ABAAADBADBAADAA设， 练习 .(P107.2) 如图， 60° 的二面角的棱上有 A 、 B 两点， 直线 AC 、 BD 分别在这个二面角的两个半平面内 , 且都垂直 AB, 已知 AB ＝ 4,AC ＝6 ，BD ＝ 8 ，求 CD 的长 . BACD68解 1 练习 .(P107.2) 如图， 60° 的二面角的棱上有 A 、 B 两点， 直线 AC 、 BD 分别在这个二面角的两个半平面内 , 且都垂直 AB, 已知 AB ＝ 4,AC ＝6 ，BD ＝ 8 ，求 CD 的长 . BACD68解 2ABCD1A1B1C1DExyz 例 如...