数学 2.4.2抛物线的简单几何性质教学课件 新人教A版选修2 1 课件VIP免费

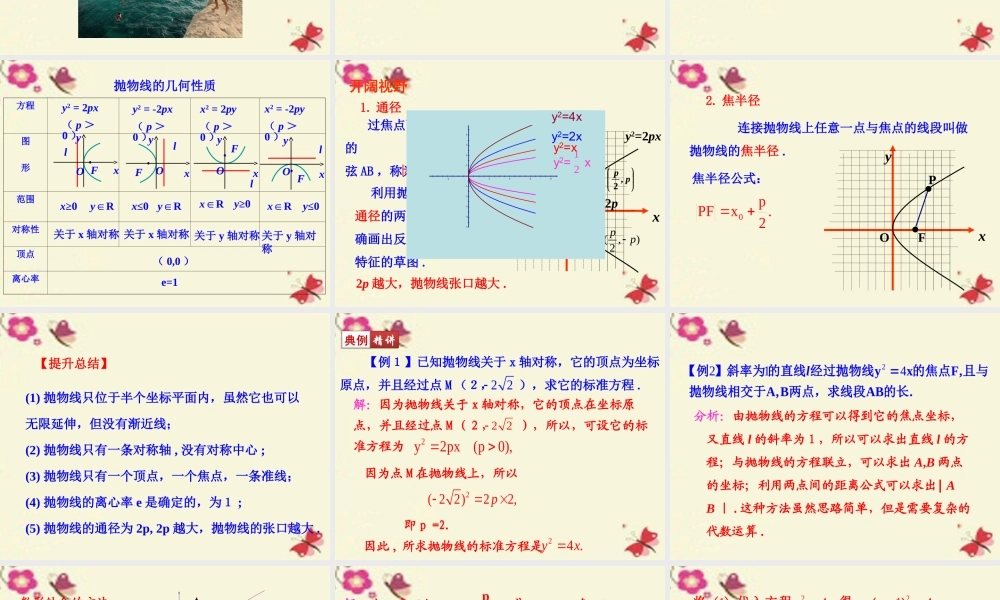
图形标准方程焦点坐标准线方程220ypx(p)220xpy(p)220xpy(p)2p(0)，2p(0,)2p(0,)220ypx(p)2p(0)，2px 2px 2py 2py 2.4.2 抛物线的简单几何性质 2.4 抛物线 抛物线有许多重要性质 . 我们根据抛物线的标准方程研究它的一些简单几何性质 .探究 抛物线的简单几何性质 )0(22ppxy方程图形范围对称性顶点离心率y2 = 2px（ p ＞0 ）y2 = -2px（ p ＞0 ）x2 = 2py（ p ＞0 ）x2 = -2py（ p ＞0 ）lFyxOlFyxOlFyxOx≥0yR∈x≤0yR∈xR∈y≥0y≤0xR∈lFyxO关于 x 轴对称 关于 x 轴对称 关于 y 轴对称关于 y 轴对称（ 0,0 ）e=1抛物线的几何性质xyOFABy2=2px2p 过焦点而垂直于对称轴的弦 AB ，称为抛物线的通径 . 利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图 .pp ,2(,)2pp|AB|=2p2p 越大，抛物线张口越大 .1. 通径4321-1-2-3-4-5-2246810y2= xy2=xy2=2xy2=4x21开阔视野 连接抛物线上任意一点与焦点的线段叫做抛物线的焦半径 .焦半径公式：xyOFP2. 焦半径0pPFx.2(1) 抛物线只位于半个坐标平面内，虽然它也可以无限延伸，但没有渐近线；(2) 抛物线只有一条对称轴 , 没有对称中心 ;(3) 抛物线只有一个顶点，一个焦点，一条准线；(4) 抛物线的离心率 e 是确定的，为１ ;(5) 抛物线的通径为 2p, 2p 越大，抛物线的张口越大 .【提升总结】解：因为抛物线关于 x 轴对称，它的顶点在坐标原点，并且经过点 M （２， ），所以，可设它的标准方程为2 22y2px(p0),因为点 M 在抛物线上，所以2( 2 2)22,p因此 , 所求抛物线的标准方程是24 .yx 【例１】已知抛物线关于 x 轴对称，它的顶点为坐标原点，并且经过点 M （２， ），求它的标准方程 .2 2即 p =2.2214yxF,A,BAB.l【例 】斜率为 的直线 经过抛物线的焦点且与抛物线相交于两点，求线段的长分析：由抛物线的方程可以得到它的焦点坐标，又直线 l 的斜率为 1 ，所以可以求出直线 l 的方程；与抛物线的方程联立，可以求出 A,B 两点的坐标；利用两点间的距离公式可以求出∣ AB ｜ . 这种方法虽然思路简单，但是需要复杂的代数运算 .数形结合的方法122ABAFBFxx.12 A,Bxx ,AB .由此可见，只要求出点的横坐标之和就可以求出xyOFABBA''xy42 1211ABAFdx,BFdx,122ABAFBF...