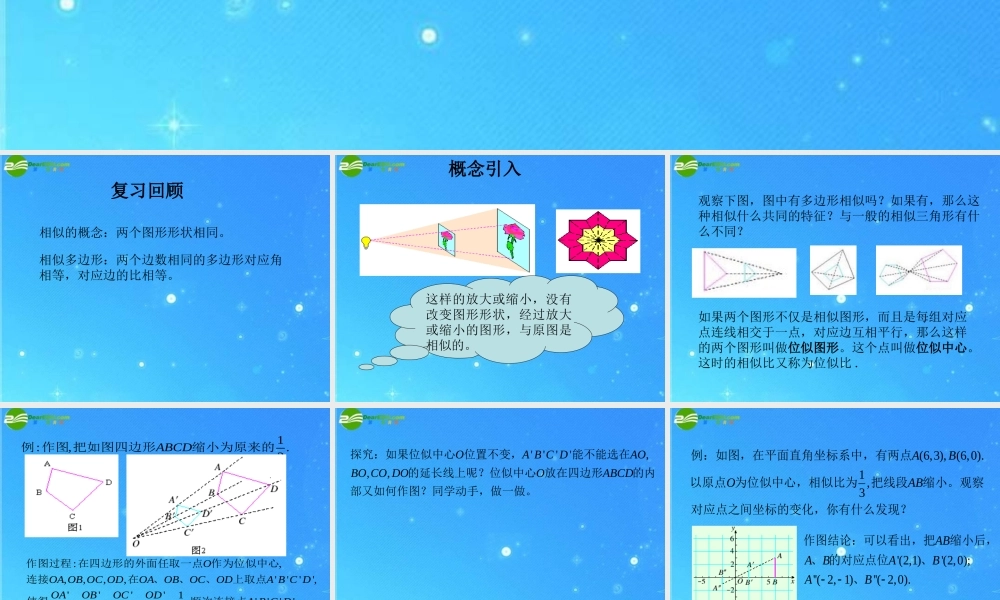
位似 复习回顾 相似的概念:两个图形形状相同。 相似多边形:两个边数相同的多边形对应角相等,对应边的比相等。 这样的放大或缩小,没有改变图形形状,经过放大或缩小的图形,与原图是相似的。概念引入观察下图,图中有多边形相似吗?如果有,那么这种相似什么共同的特征?与一般的相似三角形有什么不同? 如果两个图形不仅是相似图形,而且是每组对应点连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形。这个点叫做位似中心。这时的相似比又称为位似比 . 1:,.2ABCD例 作图 把如图四边形缩小为原来的:,,,,,'''',''''1 ,'''',2''''OOA OB OC ODOAOBOCODA B C DOAOBOCODA B C DOAOBOCODA B C D作图过程 在四边形的外面任取一点 作为位似中心连接在、、、上取点使得顺次连接点所得四边形为所求图形。'''',,,OA B C DAOBO CO DOOABCD探究:如果位似中心 位置不变,能不能选在的延长线上呢?位似中心 放在四边形的内部又如何作图?同学动手,做一做。(6,3), (6,0).1 ,3ABOAB例:如图,在平面直角坐标系中,有两点以原点 为位似中心,相似比为把线段缩小。观察对应点之间坐标的变化,你有什么发现?'(2,1)'(2,0);''( 2, 1)''( 2,0).ABABABAB作图结论:可以看出,把缩小后,、 的对应点位、、(2,3), (2,1), (6,2),2ABCABCOABC例:如图,在平面直角坐标系中,三个顶点坐标分别为以原点 为位似中心,相似比为 ,将放大,观察对应顶点坐标的变化,你有什么发现?'(4,6)'(4,2)'(12,4); ''( 4, 6)''( 4, 2)''( 12, 4)ABCA BCABCABC作图结论:可以看出,把放大后,、 、 对应点位、、、、。,kkk归纳:在平面直角坐标系中,如果位似是以原点为位似中心,相似比为那么位似图形对应点的坐标的比等于 或。( 6,6)( 8,2)( 4,0)( 2,4),ABCDABCDO例:如图,四边形的坐标分别为、、、画出它的一个以原点 为位似中心,1相似比为 的位似图形。2'( 3,3)'( 4,1)'( 2,0)'( 1,2),'''',''''ABCDABCDA B C DABCD解:如图,利用位似中对应点的坐标的变化规律,分别取、、、依次连接点、、、四边形就是要求的四边形的位似图形。''(3, 3)''(4, 11)''(2,0)''(1, 2),'''''''',''''''''ABCDABCDA B C DABCD或解:利用位似中对应点的坐标的变化规律,分别取、、、依次连接点、、、四边形就是要求的四边形的位似图形。观察教材 P63...