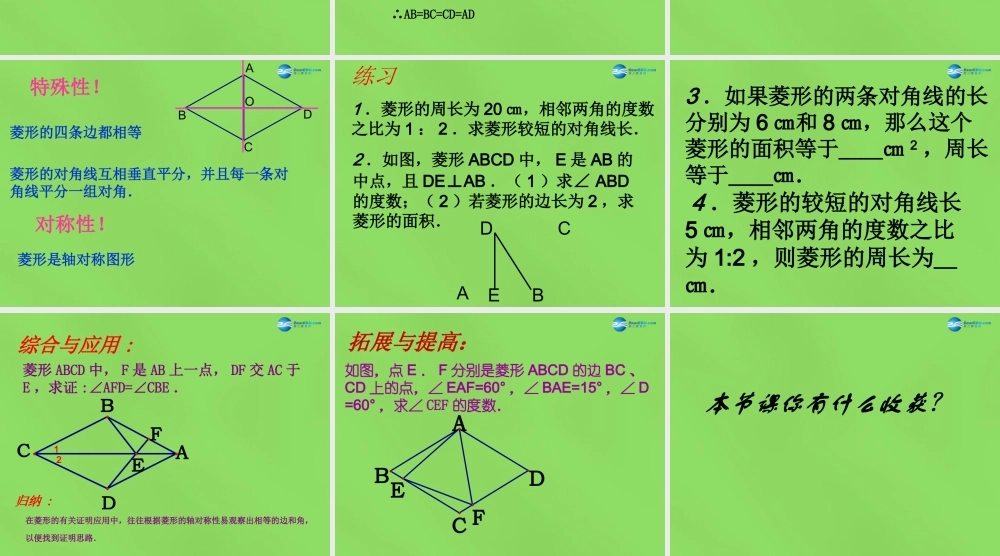
19 . 3 . 2 菱形 平行四边形 邻边相等菱形在平行四边形中,如果平移一边,得到的四边形始终是什么四边形?如果改变了边的长度,使两邻边相等,那么这个平行四边形成为怎样的四边形?让我们一同走进生活中的菱形菱形就在我们身边对边平行且相等对角相等对角线互相平分ABDC菱形是特殊的平行四边形,它具有平行四边形的一切性质.菱形的性质定理 1 :菱形的四条边都相等已知:菱形 ABCD求证: AB=BC=CD=AD证明: ∵ ABCD 是菱形 ∴AB=BC ,又 ∵ AB=CD , AD=BC ∴AB=BC=CD=ADABDC下图,已知:菱形 ABCD 的对角线 AC 和 BD 相交于点 O ,ABCDO求证: AC⊥BD ; AC 平分∠ BAD 和∠ BCD ; BD 平分∠ ABC 和∠ ADC . 菱形的对角线互相垂直 ,并且每一条对角线平分一组对角.平分菱形的性质定理 2 :菱形的四条边都相等菱形的对角线互相垂直平分,并且每一条对角线平分一组对角.DOACB特殊性!菱形是轴对称图形对称性!练习1 .菱形的周长为 20 ㎝,相邻两角的度数之比为 1 : 2 .求菱形较短的对角线长.2 .如图,菱形 ABCD 中, E 是 AB 的中点,且 DE⊥AB .( 1 )求∠ ABD的度数;( 2 )若菱形的边长为 2 ,求菱形的面积.ABCDE3 .如果菱形的两条对角线的长分别为 6 ㎝和 8 ㎝,那么这个菱形的面积等于__㎝ 2 ,周长等于__㎝. 4 .菱形的较短的对角线长5 ㎝,相邻两角的度数之比为 1:2 ,则菱形的周长为_㎝.综合与应用 :菱形 ABCD 中, F 是 AB 上一点, DF 交 AC 于E ,求证 :∠AFD=∠CBE .EBCADF归纳 :在菱形的有关证明应用中,往往根据菱形的轴对称性易观察出相等的边和角,以便找到证明思路.12拓展与提高:如图,点 E . F 分别是菱形 ABCD 的边 BC 、CD 上的点,∠ EAF=60° ,∠ BAE=15° ,∠ D=60° ,求∠ CEF 的度数.FDABCE 本节课你有什么收获?