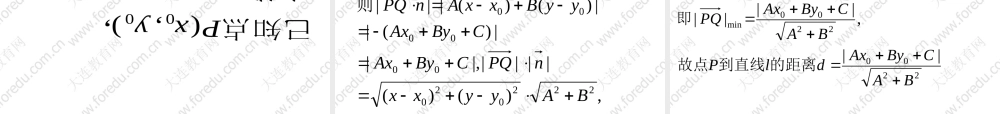向量的数量积 人教版 课件VIP免费

巧用向量的数量积的问题获得简单解答。看似复杂注意巧用向量会使一些法。如在平时解题中形的内在联系与转换方提供了数与个公式结合起来则为纯“数字化”，两形”的特征，而公式有明显的向量的数量积公式：,cos||||"cos||||21212121yyxxbabayyxxbababa 的值域x4x4x4x5例1求函数f(x)221 、用于函数|cosθb||a|ba]因为43π，4π[则θ夹角为θ，b与a其中),x4x4,x4x5(b1),(1,a解令22 3，3][函数f(x)得值域为3,||f(x)所以32223||c0sθ23||cosθx4x4x4x52||f(x)即|||cosθb||a||ba|所以22 2 、证明不等式Rdcba,,, 2 已知例))((2222dcbabdac求证))((||||cos||||),(),,(:2222dcbabdacnmnmnmdcnbam即则设证明 1||1,1,,,32222bdacdcbaRdcba求证且已知例coscos||||,1||||),,(),,(nmnmnmnmdcnbam因为则的夹角为与证明设 时等号成立即当且仅当此时共线时等号成立与也就是，或即当且仅当即所以bcadbcadnmbdacnm0,01|cos|,1||1|cos||| axaxy求的最小值为若函数例1,4cossin243 、求三角函数最值514444,4||||||||||)sin,(cos),2,(aaayanmnmnmnmnmnam解得由题意得故得由解设 的最大值试求的所有等差数列：对满足条件和正数给定正整数例12213212121,,,,5nnnnaaaSaaaMaaMn4 、用于数列 ）所以因为解由题意得1111211213(212,2))(1(aanSaaaaanSnnnnn MnSMaaaaaaMnaannmnmaanmnnnnn10213,031021|3|21||||||),,(),1,3(max212111111111此时，上式中两等号同时成立时且且当得由令 5 、用于平面几何问题垂直证明菱形的对角线互相例6BDACBDACABCD求证：它的对角线是与为菱形，已知：, BDACABBCABBCBCABBDACABBCABADBDBCABAC所以所以证明：因为0||||))((22 身手。在解析几何中更是大显，“数”与“形”的特征由于向量的数量积兼有6 、用于解析几何2,,,)0(272BFABABABAFppxy求证：向准线作垂线，得垂足自两点，的直线交抛物线与的焦点过抛物线例 20,,),,2(),2(,,,)0,2(2212122121...