北京市东城区普通校2019届高三3月联考(零模)数学理试题VIP免费

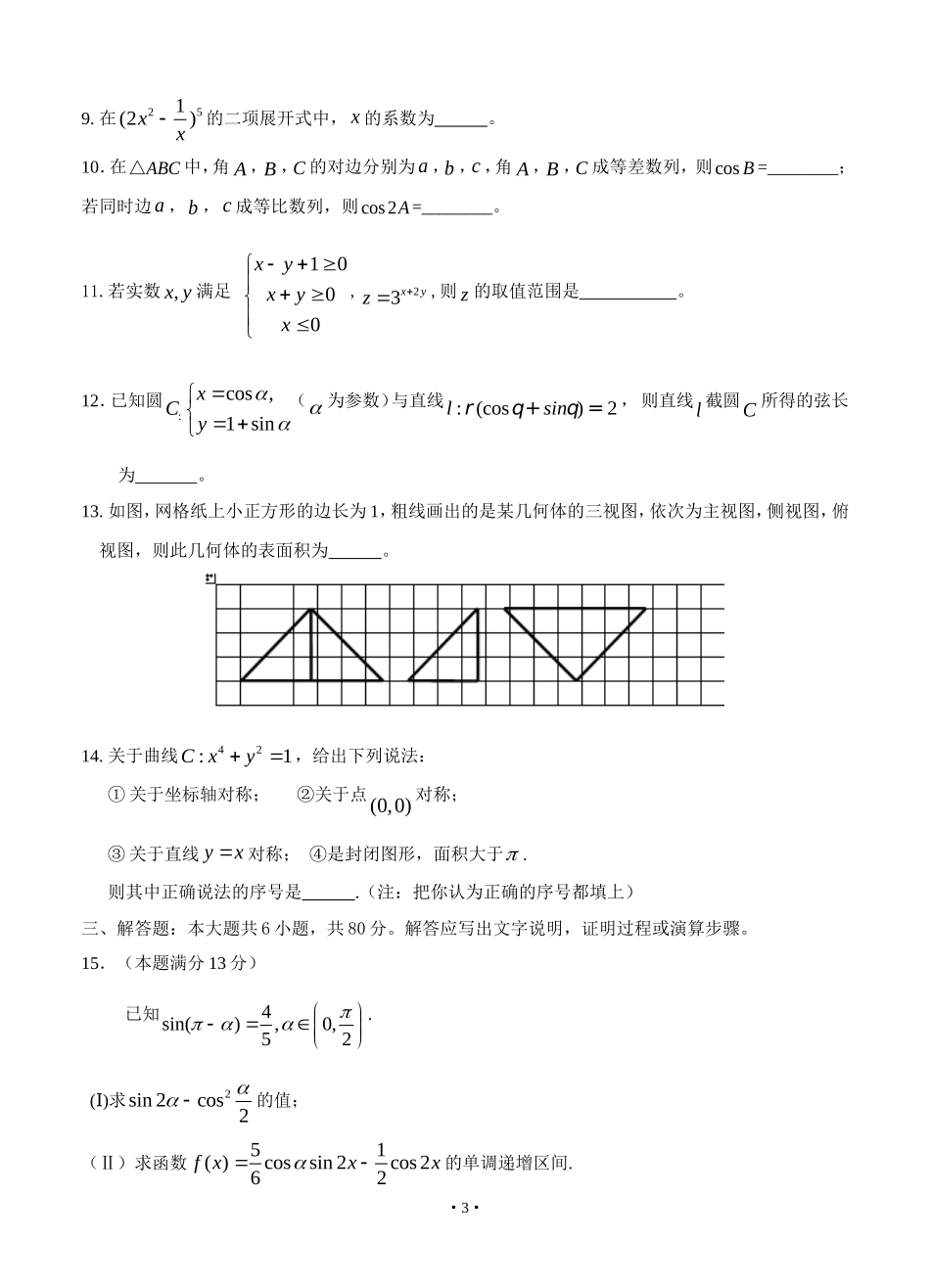
北京市东城区普通校2019届高三3月联考（零模）数学（理科）本试卷共150分，考试用长120分钟。第一部分一、选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设集合ln1Axyx,集合2Byyx,则ABA.0,1B.0,1C.,1D.,12.函数2()logfxx与11()()2xgx在同一直角坐标系中的图象是ABCD3.已知函数()sin()(0)4fxx的最小正周期为，则该函数的图象A.关于点(,0)4对称B.关于直线8x对称C.关于点(,0)8对称D.关于直线4x对称4.若双曲线221xky的离心率是2，则实数k的值是A.3B.13C.3D.135.某程序框图如图所示,若输出的S=57，则判断框内为A.6kB.5k·1·C.4kD.3k6.设aR，函数32()(3)fxxaxax的导函数是()fx，若()fx是偶函数，则曲线()yfx在原点处的切线方程为A.3yxB.2yxC.3yxD.2yx7.如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为A.71B.61C.51D.418.从一个三棱柱的6个顶点中任取4个做为顶点，能构成三棱锥的个数设为m；过三棱柱任意两个顶点的直线(15条)中，其中能构成异面直线有n对，则mn，的取值分别为A.15，45B.10,30C.12,36D.12,48第二部分二、填空题：本大题共6小题,每小题5分，共30分,把答案填在题中横线上。·2·9.在251(2)xx的二项展开式中，x的系数为。10．在ABC△中，角A，B，C的对边分别为a，b，c，角A，B，C成等差数列，则cosB=________；若同时边a，b，c成等比数列，则cos2A=________。11.若实数,xy满足1000xyxyx,23xyz,则z的取值范围是。12．已知圆:cos,1sinxCy（为参数）与直线:(cos)2lsinrqq+=，则直线l截圆C所得的弦长为。13.如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，依次为主视图，侧视图，俯视图，则此几何体的表面积为。14.关于曲线42:1Cxy，给出下列说法：①关于坐标轴对称；②关于点(0,0)对称；③关于直线yx对称；④是封闭图形，面积大于.则其中正确说法的序号是.（注：把你认为正确的序号都填上）三、解答题：本大题共6小题，共80分。解答应写出文字说明，证明过程或演算步骤。15．（本题满分13分）已知4sin(),0,52.()Ⅰ求2sin2cos2的值；（Ⅱ）求函数51()cossin2cos262fxxx的单调递增区间.·3·16.（本题满分13分）一个袋中装有6个形状大小完全相同的小球，球的编号分别为1,2,3,4,5,6.()Ⅰ若从袋中每次随机抽取1个球，有放回的抽取3次，求恰有两次编号为3的倍数的概率；（Ⅱ）若一次从袋中随机抽取3个球，记球的最大编号为X，求随机变量X的分布列和X的数学期望.17.（本题满分14分）如图，已知菱形ABCD的边长为6，60BAD,ACBDO.将菱形ABCD沿对角线AC折起，使32BD，得到三棱锥BACD.()Ⅰ若点M是棱BC的中点，求证://OM平面ABD；（Ⅱ）求二面角ABDO的余弦值；（Ⅲ）设点N是线段BD上一个动点，试确定N点的位置，使得42CN，并证明你的结论.18.（本题满分13分）已知函数21()(21)2ln(0)2fxaxaxxa.()Ⅰ当0a时，求()fx的单调区间；()Ⅱ求()yfx在区间(0,2]上的最大值.19.（本题满分13分）已知直线l与抛物线24xy相交于A，B两点，且与圆22(1)1yx相切.（Ⅰ）求直线l在y轴上截距的取值范围；（Ⅱ）设F是抛物线的焦点，且0FAFB�，求直线l的方程.20.（本题满分14分）在数列{}na和{}nb中，nnaa，(1)nbanb，1,2,3,n，其中2a且·4·aZ，bR.（Ⅰ）若11ab，22ab，求数列{}nb的前n项和；（Ⅱ）证明：当2,2ab时，数列{}nb中的任意三项都不能构成等比数列；（Ⅲ）设123{,,,}Aaaa，123{,,,}Bbbb，设CAB.当1b时，求出相应的集合C.·5·北京市东城区普通校2019届高三3月联考（零模）数学理参考答案一、选择题：本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.题号12345678答案ABBDCABC二、填空题：本大题共6小题,每小题5分,共30分,把答案填在题...