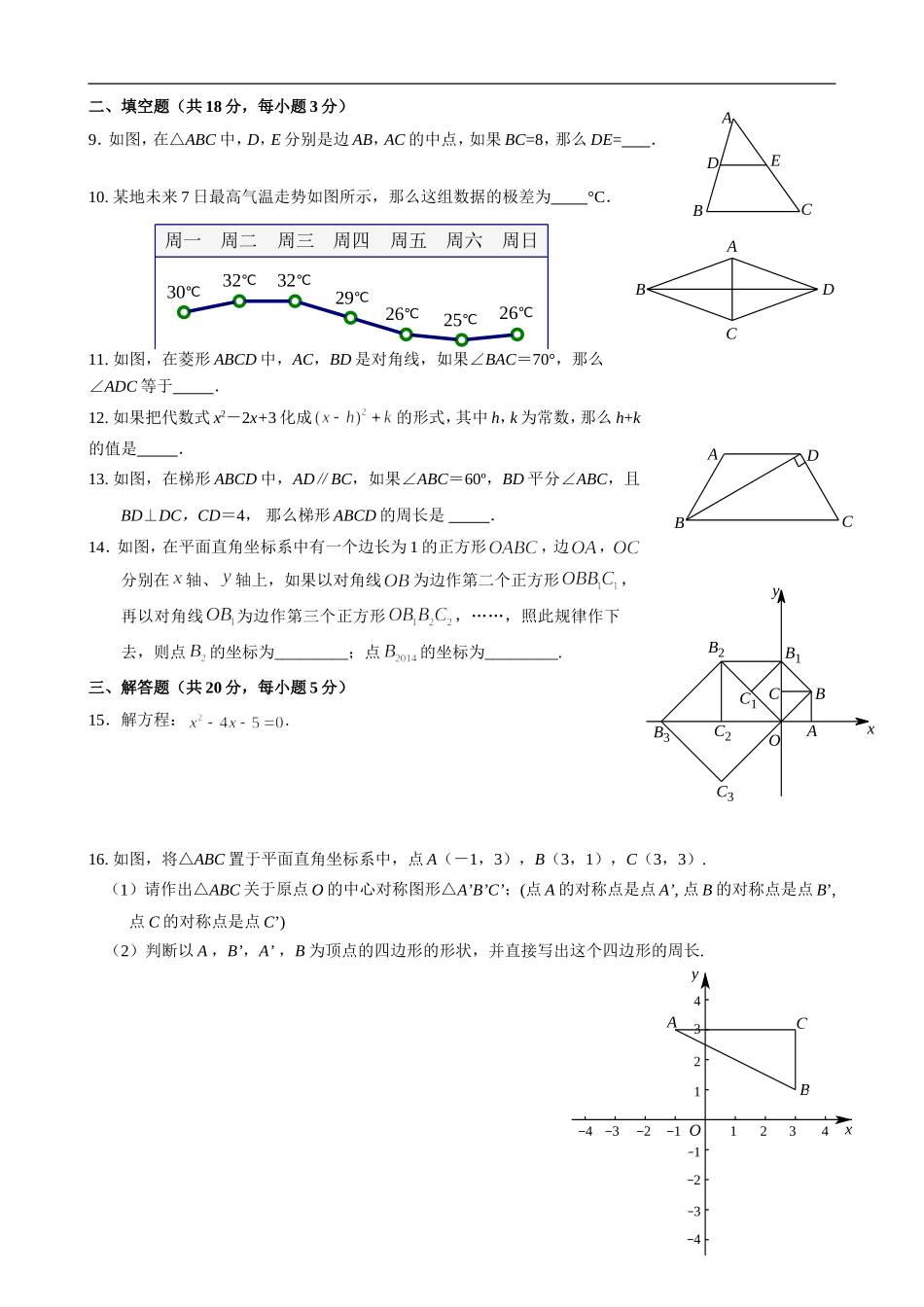
534121xO6y2534121xO6y2MPDCBA丰台区2013—2014学年度第二学期期末统考初二数学一、选择题(共24分,每小题3分)下列各题均有四个选项,其中只有一个是符合题意的.1.函数中自变量的取值范围是A.B.C.D.2.五边形的内角和为A.180°B.360°C.540°D.720°3.在平面直角坐标系中,点A(1,2)关于x轴对称的点的坐标是A.(1,2)B.(1,-2)C.(-1,2)D.(-1,-2)4.下列图形中,既是中心对称图形又是轴对称图形的是A.等边三角形B.平行四边形C.等腰梯形D.矩形5.已知2x是一元二次方程的一个解,则m的值是A.B.C.D.2或6.某工厂由于管理水平提高,生产成本逐月下降.原来每件产品的成本是1600元,两个月后,降至900元.如果产品成本的月平均降低率是x,那么根据题意所列方程正确的是A.B.C.D.7.10名同学分成甲、乙两队进行篮球比赛,他们的身高(单位:cm)如下表所示:队员1队员2队员3队员4队员5甲队173175175175177乙队170171175179180设两队队员身高的平均数依次为,,身高的方差依次为,,则下列关系中完全正确的是A.,B.,C.,D.,8.如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是ABCD534121xO6y2534121xO6y226℃25℃26℃29℃32℃32℃30℃周日周五周六周四周三周二周一4444123123321213CBAxOy二、填空题(共18分,每小题3分)9.如图,在△ABC中,D,E分别是边AB,AC的中点,如果BC=8,那么DE=.10.某地未来7日最高气温走势如图所示,那么这组数据的极差为°C.11.如图,在菱形ABCD中,AC,BD是对角线,如果∠BAC=70°,那么∠ADC等于.12.如果把代数式x2-2x+3化成的形式,其中h,k为常数,那么h+k的值是.13.如图,在梯形ABCD中,AD∥BC,如果∠ABC=60º,BD平分∠ABC,且BD⊥DC,CD=4,那么梯形ABCD的周长是.14.如图,在平面直角坐标系中有一个边长为1的正方形,边,分别在轴、轴上,如果以对角线为边作第二个正方形,再以对角线为边作第三个正方形,……,照此规律作下去,则点的坐标为_________;点的坐标为_________.三、解答题(共20分,每小题5分)15.解方程:.16.如图,将△ABC置于平面直角坐标系中,点A(-1,3),B(3,1),C(3,3).(1)请作出△ABC关于原点O的中心对称图形△A’B’C’;(点A的对称点是点A’,点B的对称点是点B’,点C的对称点是点C’)(2)判断以A,B’,A’,B为顶点的四边形的形状,并直接写出这个四边形的周长.EDCBAABCDC1C2C3CBB3B2B1AxOyDCBA17.已知一次函数的图象与轴交于点,与轴交于点.(1)求,两点的坐标;(2)过点作直线P与x轴交于点,且使△AP的面积为2,求点P的坐标.18.已知:如图,点E,F是□ABCD中AB,DC边上的点,且AE=CF,联结DE,BF.求证:DE=BF.四、解答题(共24分,每小题6分)19.已知关于的一元二次方程有两个不相等的实数根.(1)求的取值范围;(2)若为正整数,且该方程的根都是整数,求的值.20.为了解某校学生的身高情况,随机抽取该校若干名学生测量他们的身高,已知抽取的学生中,男生、女生的人数相同,利用所得数据绘制如下统计图表:身高分组表女生身高频数分布表男生身高频数分布直方图身高/cm146102EDCB4812频数A请根据以上图表提供的信息,解答下列问题:(1)在女生身高频数分布表中:=,=,=;(2)补全男生身高频数分布直方图;(3)已知该校共有女生400人,男生380人,请估计身高在165≤<170之间的学生约有多少人.21.为鼓励居民节约用水,某市对居民用水收费实行“阶梯水价”,按每年用水量统计,不超过180立方米的部分按每立方米5元收费;超过180立方米不超过260立方米的部分按每立方米7元收费;超过组别身高/cmABCDE组别频数频率A8B120.30C100.25D0.15E40.10合计1.00ABCDEF260立方米的部分按每立方米9元收费.(1)设每年用水量为x立方米,按“阶梯水价”应缴水费y元,请写出y(元)与x(立方米)之间的函数解析式;(2)明明家预计2015年全年用水量为200立方米,那么按“阶梯水价”收费,她家应缴水费多少元?22.如图,矩形ABCD的对...