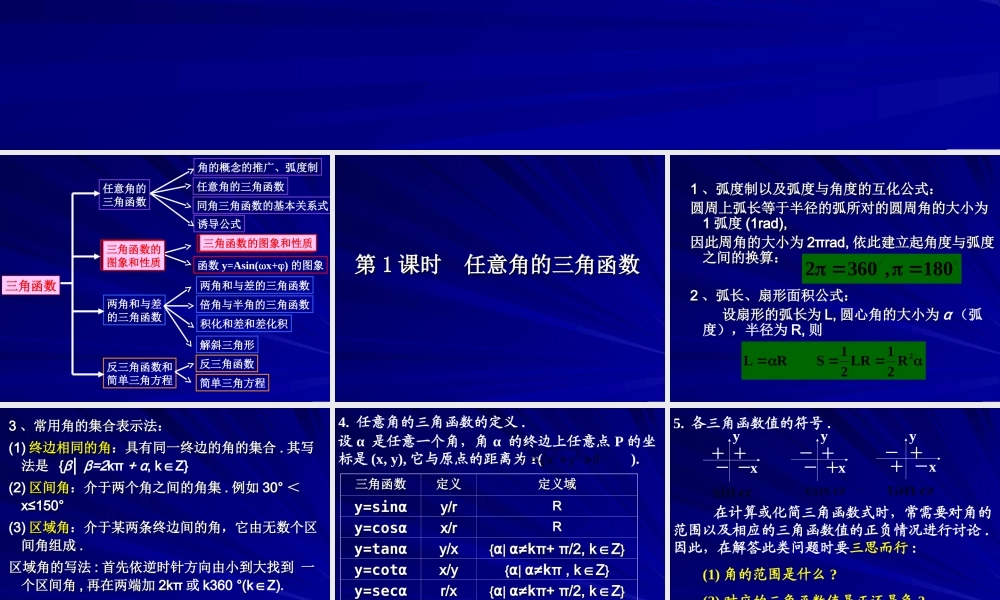
第四章 三角函数 任意角的三角函数三角函数的图象和性质两角和与差的三角函数反三角函数和简单三角方程三角函数角的概念的推广、弧度制任意角的三角函数同角三角函数的基本关系式诱导公式函数 y=Asin(x+) 的图象三角函数的图象和性质积化和差和差化积倍角与半角的三角函数两角和与差的三角函数解斜三角形简单三角方程反三角函数三角函数的图象和性质三角函数的图象和性质 第第 11 课时 任意角的三角函数课时 任意角的三角函数 11 、弧度制以及弧度与角度的互化公式:、弧度制以及弧度与角度的互化公式:圆周上弧长等于半径的弧所对的圆周角的大小为圆周上弧长等于半径的弧所对的圆周角的大小为11 弧度弧度 (1rad),(1rad),因此周角的大小为因此周角的大小为 2πrad,2πrad, 依此建立起角度与弧度依此建立起角度与弧度之间的换算:之间的换算:22 、弧长、扇形面积公式:、弧长、扇形面积公式: 设扇形的弧长为设扇形的弧长为 L,L, 圆心角的大小为圆心角的大小为 α (弧度),半径为 R, 则180,36022R21LR21SRL 33 、常用角的集合表示法:、常用角的集合表示法:(1)(1) 终边相同的角终边相同的角:具有同一终边的角的集合:具有同一终边的角的集合 .. 其写其写法是 法是 {{β│ β=2kπ + α, kZ}∈(2)(2) 区间角区间角:介于两个角之间的角集:介于两个角之间的角集 .. 例如例如 30°30° <<x≤150°x≤150°(3)(3) 区域角区域角:介于某两条终边间的角,它由无数个区:介于某两条终边间的角,它由无数个区间角组成间角组成 ..区域角的写法区域角的写法 :: 首先依逆时针方向由小到大找到 一首先依逆时针方向由小到大找到 一个区间角个区间角 ,, 再在两端加再在两端加 2k2kπ 或 k360 °(°(kZ).∈ 如 :2kπ+π/6<α<2kπ+π/3, kZ.∈(4)(4) 象限角象限角与与轴线角轴线角:一种特殊的区域角:一种特殊的区域角 .. 4. 任意角的三角函数的定义 .设 α 是任意一个角,角 α 的终边上任意点 P 的坐标是 (x, y), 它与原点的距离为 r( ).022yxr三角函数三角函数定义定义定义域定义域y=sinαy=sinαy/ry/rRRy=cosαy=cosαx/rx/rRRy=tanαy=tanαy/xy/x{{αα| | α≠kα≠kπ+ π/2, kZ∈π+ π/2, kZ∈ }}y=cotαy=cotαx/yx/y{{αα| | α≠kα≠kπ , kZ∈π , kZ∈ }}y=secαy=secαr/xr/x{{αα| | α≠kα≠kπ+ π/2,...