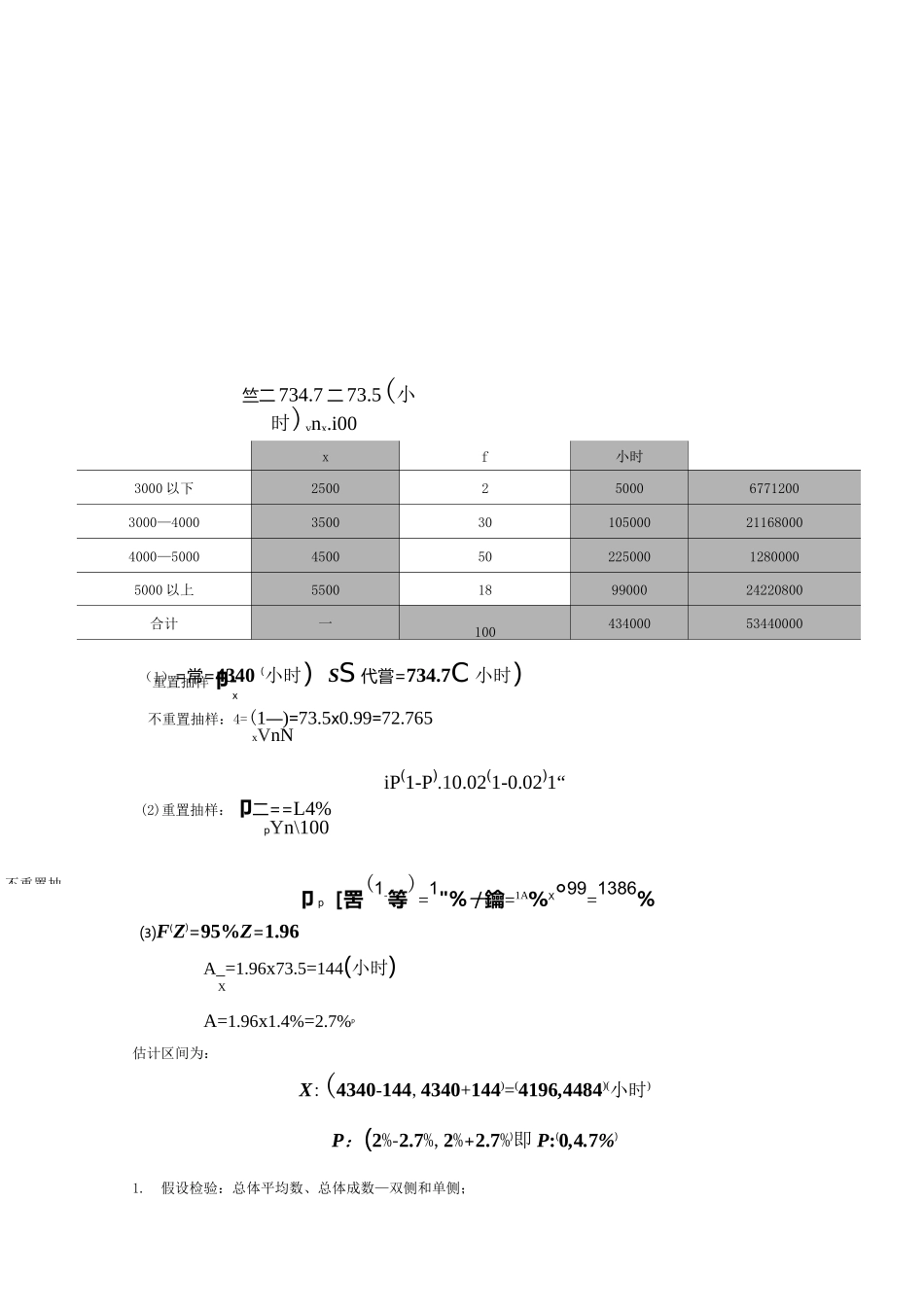
练习 1.采用简单随机重置抽样的方法,从 2000 件产品中抽查 200 件,其中合格品 190 件。要求(1)计算合格品率及其抽样平均误差。(2)以 95.45%概率保证程度,对合格品率和合格品数目进行区间估计。(3)如果合格品率的极限误差为 2.31%,则其概率保证程度是多少?解:已知N=2000(f 牛)n=200(f 牛)F(Z)=95・45%A=2.31%G)样本合格频率为:“弟=95%、pEp=]:° ・ 95 G 一 ° ・ 95 ) =1.54%n200(2)F(Z)=0.9546%Z=2A=Z 屮=2x1.54%=3.08%产品合格率的估计区间:P:(95%-3・08%,95%+3・08%)=(91・92%,98・08%)合格产品数估计区间:NP:(2000x91.92%2000x98・08%)=(1838,1961)(件)G)A=Z•卩 Z=A==1.5F(Z)=F(1・5)=86・64%卩 1.54%练习 2.某电子产品的使用寿命在 3000 小时以下为次品,现在用简单随机抽样方法,从 5000 个产品中抽取 100 个对其使用寿命进行测试,其结果如下:电子产品使用寿命表根据以上资料,要求:(1)按重置抽样和不重置抽样计算该产品平均寿命的抽样平均误差。(2)按重置抽样和不重置抽样计算该产品次品率的抽样平均误差。(3)以 95%的概率保证程度,对该产品的平均使用寿命和次品率进行区间估计解:使用寿命(小时)产品个数xf分组组中值(个)A—X7f竺二 734.7 二 73.5(小时)vnx.i00不重置抽xf小时3000 以下25002500067712003000—4000350030105000211680004000—500045005022500012800005000 以上5500189900024220800合计一10043400053440000(1)=常=4340(小时)SS 代嘗=734.7C 小时)不重置抽样:4=(1—)=73.5x0.99=72.765xVnNiP(1-P).10.02(1-0.02)1“(2)重置抽样:卩二==L4%pYn\100卩 p[罟(1-等)=1"%十鑰=1A%X°99=1386%⑶F(Z)=95%Z=1.96A_=1.96x73.5=144(小时)XA=1.96x1.4%=2.7%p估计区间为:X:(4340-144,4340+144)=(4196,4484)(小时)P:(2%-2.7%,2%+2.7%)即 P:(0,4.7%)1.假设检验:总体平均数、总体成数—双侧和单侧;重置抽样卩-x练习 3.某牌号的彩电规定无故障时间为 10000 小时,厂家采取改正措施,现在从新批量彩电中抽取 100 台,测得平均无故障时间为 10150 小时,标准差为 500 小时,能否据此判断该彩电无故障时间有显著增加(a 二 0.01)?解:已知:X0=10000(小时)n 二 100(件)X=10150(小时)Q(X)=500(小时)a=0.01(大样本)p—PP(1—P)_—0.577设:H°:X=10000H:X>10000(单侧、Z 检验)1a、二 0.01F(Z)=1-2x0.01 二...